题目内容
【题目】已知向量 
=（cosx，﹣1）， 
=（ 
sinx，cos2x），设函数f（x）= + 
．
（Ⅰ）求函数f（x）的最小正周期和单调递增区间；
（Ⅱ）当x∈（0， 
）时，求函数f（x）的值域．
【答案】解：（Ⅰ）依题意向量 
=（cosx，﹣1）， 
=（ 
sinx，cos2x）， 函数f（x）= + 
= 
= 
．
得 
∴f（x）的最小正周期是：T=π…
由 
解得 
，k∈Z．
从而可得函数f（x）的单调递增区间是： 
（Ⅱ）由 
，可得 
从而可得函数f（x）的值域是： 
【解析】（Ⅰ）利用已知条件通过向量的数量积求出函数的解析式，求才函数的周期以及单调增区间．（Ⅱ）利用角的范围，求出相位的范围，然后求出值域．
【考点精析】解答此题的关键在于理解正弦函数的单调性的相关知识，掌握正弦函数的单调性：在
上是增函数；在
上是减函数．
练习册系列答案
相关题目
【题目】大学生赵敏利用寒假参加社会实践，对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x元和销售量y件之间的一组数据如表所示：
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
（1）根据7至11月份的数据，求出y关于x的回归直线方程；
（2）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？ 参考公式：回归直线方程 
=b 
+a，其中b=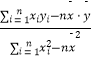 
．
参考数据： 
=392， 
=502.5．
