题目内容
【题目】关于下列命题:
①函数y=tanx的一个对称中心是( ![]() ,0);
,0);
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一条对称轴是x=﹣
)的一条对称轴是x=﹣ ![]() ;
;
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数.
]上是增函数.
写出所有正确的命题的题号 .
【答案】①③
【解析】解:对于函数y=tanx,当x= ![]() 时,y无意义,故y=tanx的图象的一个对称中心是(
时,y无意义,故y=tanx的图象的一个对称中心是( ![]() ,0),故①正确.
,0),故①正确.
∵函数y=cos2( ![]() ﹣x)=cos(
﹣x)=cos( ![]() ﹣2x)=sin2x,故它是奇函数,故②错误;
﹣2x)=sin2x,故它是奇函数,故②错误;
令2x﹣ ![]() =kπ+
=kπ+ ![]() ,k∈Z,求得x=
,k∈Z,求得x= ![]() +
+ ![]() ,可得函数y=4sin(2x﹣
,可得函数y=4sin(2x﹣ ![]() )的一条对称轴是x=﹣
)的一条对称轴是x=﹣ ![]() ,故③正确;
,故③正确;
在区间[﹣ ![]() ,
, ![]() ]上,x+
]上,x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],函数y=sin(x+
],函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上没有单调性,故④错误,
]上没有单调性,故④错误,
所以答案是:①③.

 名校课堂系列答案
名校课堂系列答案【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如表:
(单位:万件)之间的关系如表:
| 1 | 2 | 3 | 4 |
| 12 | 28 | 42 | 56 |
(Ⅰ)在图中画出表中数据的散点图;
(Ⅱ)根据(Ⅰ)中的散点图拟合![]() 与
与![]() 的回归模型,并用相关系数甲乙说明;
的回归模型,并用相关系数甲乙说明;
(Ⅲ)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量约为多少?.
的回归方程,预测第5年的销售量约为多少?.
附注:参考数据: 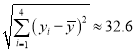 ,
, ![]() ,
, ![]() .
.
参考公式:相关系数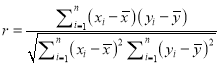 ,
,
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
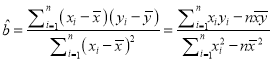 ,
, ![]() .
.
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.