题目内容
14.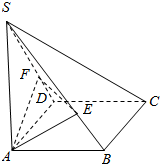 如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A分别作AE⊥SB,AF⊥SD,垂足分别为点E和点F,求证:EF⊥SC.
如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A分别作AE⊥SB,AF⊥SD,垂足分别为点E和点F,求证:EF⊥SC.
分析 证明SC⊥平面AEF,即可得到EF⊥SC.
解答 证明:∵SA⊥平面ABCD,
∴SA⊥BC.
∵AB⊥BC,且SA∩AB=A,
∴BC⊥平面SAB,
∴BC⊥AE,
又∵AE⊥SB,且SB∩BC=B,
∴AE⊥平面SBC,
∴AE⊥SC,
同理AF⊥SC,
∵AE∩EF=E,
∴SC⊥平面AEF,EF?平面AEF,
∴EF⊥SC.
点评 本题重点考查了空间中直线与直线垂直、直线与平面垂直、平面与平面垂直的判定和性质等知识,属于基本知识的考查,属于中档题.

练习册系列答案
相关题目
4.函数y=x4+$\frac{1}{x^4}$的图象关于 ( )对称.
| A. | 原点 | B. | y轴 | C. | x轴 | D. | 直线y=x |