题目内容
9．函数y=$\frac{ax+2}{x+2}$在（-2，+∞）上单调递增，求实数a的范围．分析 分离常数，将原函数变成y=$a+\frac{2-2a}{x+2}$，由该函数在（-2，+∞）上单调递增，从而根据反比例函数的单调性知，2-2a＜0，解该不等式即可得出实数a的范围．
解答 解：$y=\frac{ax+2}{x+2}=\frac{a（x+2）+2-2a}{x+2}$=$a+\frac{2-2a}{x+2}$；
该函数在（-2，+∞）上单调递增；
∴根据反比例函数的单调性得：2-2a＜0；
∴a＞1；
∴实数a的范围为（1，+∞）．
点评 考查增函数的定义，分离常数法的运用，以及反比例函数的单调性，知道该函数和反比例函数y=$\frac{2-2a}{x+2}$的单调性相同．
练习册系列答案
小学期末标准试卷系列答案
相关题目
19．我们知道，对任意实数x，2x都是一个确定的实数，类似的，在下列说法中，错误的是（ ）
| A． | 对任意无理数x，5x都是一个确定的实数 | |
| B． | 对于负数x，πx没有意义 | |
| C． | 设a＞0，且a≠1，则ax中的x可以取到任意实数 | |
| D． | 若a＜0，则当x=$\frac{1}{2n}$，n∈N*时，ax没有意义 |
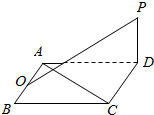
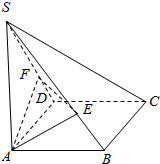如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD所在的平面，过点A分别作AE⊥SB，AF⊥SD，垂足分别为点E和点F，求证：EF⊥SC．