题目内容
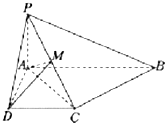 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB=
| 2 |
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥C-MAD的体积.
分析:(1)利用线面平行的判定定理证明;
(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,
计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.
(2)利用勾股定理证明BC⊥AC,由PA⊥平面ABCD,可得PA⊥BC.从而可证得BC⊥平面PAC:
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形,AE=DC,AD=EC.求得CE,
计算△ACD的面积,根据M到平面ADC的距离是P到平面ADC距离的一半,求得棱锥的高,代入体积公式计算.
解答: 解:(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
解:(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
∴AB∥CD,
又AB?平面PCD,CD?平面PCD,
∴AB∥平面PCD.
(2)∵∠ABC=45°,CB=
,AB=2,
∴AC2=AB2+BC2-2AB•BC•cos45°=4+2-2×2×
×
=2.
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC.
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BC•cos45°=
×
=1,
CE=BC•sin45°=
×
=1,∴AE=AB-BE=2-1=1
∴S△ADC=
DC•CE=
×1×1=
.,
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC-MAD=VM-ACD=
×S△ACD×(
PA)=
×
×
=
.
 解:(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,
解:(1)∵底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,∴AB∥CD,
又AB?平面PCD,CD?平面PCD,
∴AB∥平面PCD.
(2)∵∠ABC=45°,CB=
| 2 |
∴AC2=AB2+BC2-2AB•BC•cos45°=4+2-2×2×
| 2 |
| ||
| 2 |
则AC2+BC2=AB2,∴BC⊥AC.
∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC.
又PA∩AC=A,∴BC⊥平面PAC.
(3)在直角梯形ABCD中,过C作CE⊥AB于点E,
则四边形ADCE为矩形,∴AE=DC,AD=EC.
在Rt△CEB中,可得BE=BC•cos45°=
| 2 |
| ||
| 2 |
CE=BC•sin45°=
| 2 |
| ||
| 2 |
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵M是PC的中点,∴M到平面ADC的距离是P到平面ADC距离的一半,
∴VC-MAD=VM-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
点评:本题考查了线面平行的判定,线面垂直的判断,考查了三棱锥的换底性及棱锥的体积公式,涉及知识较多,对学生的推理论证能力有一定的要求.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,