题目内容
19.已知函数f(x)=Asin(ωx+φ)的最大值为2,最小正周期为π,直线x=$\frac{π}{6}$是其图象的一条对称轴,求函数g(x)=f(x-$\frac{π}{12}$)-f(x+$\frac{π}{12}$)的单调递增区间.分析 利用已知条件求出函数的解析式,然后利用两角和的正弦函数化简解析式利用正弦函数的单调性求解单调增区间即可.
解答 解:函数f(x)=Asin(ωx+φ)的最大值为2,A=2;
最小正周期为π,可得ω=2,
直线x=$\frac{π}{6}$是其图象的一条对称轴,不妨得$2×\frac{π}{6}+φ=\frac{π}{2}$,φ=$\frac{π}{6}$.
函数f(x)=2sin(2x+$\frac{π}{6}$).
函数g(x)=f(x-$\frac{π}{12}$)-f(x+$\frac{π}{12}$)=2sin2x-2sin(2x+$\frac{π}{3}$)
=2sin2x-2sin2xcos$\frac{π}{3}$-2cos2xsin$\frac{π}{3}$
=sin2x-$\sqrt{3}$cos2x
=2sin(2x-$\frac{π}{6}$).
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
函数的单调递增区间[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
点评 本题考查三角函数的解析式的求法,函数的单调增区间的求法,考查两角和与差的三角函数,计算能力.

练习册系列答案
相关题目
14.如图是某个闭合电路的一部分,每个元件正常工作的概率为$\frac{1}{2}$,则从A到B这部分电路能正常工作的概率为( )
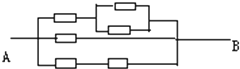

| A. | $\frac{27}{32}$ | B. | $\frac{55}{64}$ | C. | $\frac{115}{128}$ | D. | $\frac{49}{64}$ |