题目内容
8．已知三棱锥P-ABC中，△ABC为等边三角形，且PA=8，PB=PC=$\sqrt{73}$，AB=3，则三棱锥P-ABC外接球的表面积为76π．分析 先判断PA⊥平面ABC，△ABC的外接圆的半径为$\frac{\sqrt{3}}{3}×3$=$\sqrt{3}$，再利用勾股定理求出三棱锥P-ABC外接球的半径，即可求出三棱锥P-ABC外接球的表面积．
解答 解：由题意，PA⊥AB，PA⊥AC，
∴PA⊥平面ABC，
△ABC的外接圆的半径为$\frac{\sqrt{3}}{3}×3$=$\sqrt{3}$
设三棱锥P-ABC外接球的半径为R，则R2=$（\sqrt{3}）^{2}+{4}^{2}$=19，
∴三棱锥P-ABC外接球的表面积为4πR2=76π．
故答案为：76π．
点评 本题考查求三棱锥P-ABC外接球的表面积，考查学生的计算能力，确定三棱锥P-ABC外接球的半径是关键．
练习册系列答案
相关题目
19．已知抛物线方程为y=4x2，则该抛物线的焦点坐标为（ ）
| A． | （0，1） | B． | $（0，\frac{1}{16}）$ | C． | （1，0） | D． | $（\frac{1}{16}，0）$ |
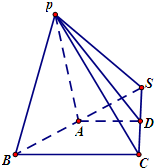在三棱锥P-SBC中，A，D分别为边SB，SC的中点，AB=2，BC=4，CD=2$\sqrt{2}$．平面PSB⊥平面ABCD，平面PAD⊥平面ABCD．