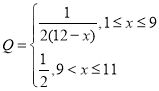题目内容
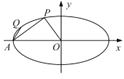
【题目】已知抛物线![]() ,过焦点
,过焦点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,
,![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的准线上一点,且
的准线上一点,且![]() 的面积为4.
的面积为4.
(1)求抛物线![]() 的标准方程.
的标准方程.
(2)设![]() ,若点
,若点![]() 是抛物线
是抛物线![]() 上的任一动点,则是否存在垂直于
上的任一动点,则是否存在垂直于![]() 轴的定直线被以
轴的定直线被以![]() 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
【答案】(1)![]() ;(2)存在,直线方程为
;(2)存在,直线方程为![]() ,弦长为2.
,弦长为2.
【解析】
(1)由![]() ,可求出
,可求出![]() ,即可得到抛物线
,即可得到抛物线![]() 的标准方程;(2)设存在直线
的标准方程;(2)设存在直线![]() :
:![]() 满足条件,
满足条件,![]() ,从而可表示出以
,从而可表示出以![]() 为直径的圆的半径和圆心,及圆心到直线
为直径的圆的半径和圆心,及圆心到直线![]() 的距离
的距离![]() ,则圆的弦长为
,则圆的弦长为![]() ,列出对应的表达式即可得到当
,列出对应的表达式即可得到当![]() 时,弦长为定值。
时,弦长为定值。
解:(1)易得![]() .
.
所以![]() .
.
![]()
(2)设存在直线![]() :
:![]() 满足条件,
满足条件,![]()
则![]() 的中点
的中点![]() ,
,![]()
因此以![]() 为直径的圆的半径
为直径的圆的半径![]()
![]() 点到直线
点到直线![]() 的距离
的距离![]()
![]() 所截弦长为
所截弦长为![]()
![]()
![]()
要使弦长与变量![]() 无关,则令
无关,则令![]() 即
即![]() 时,弦长为定值2,
时,弦长为定值2,
这时直线方程为![]() .
.
故存在垂直于![]() 轴的定直线
轴的定直线![]() ,被以
,被以![]() 为直径的圆截得的弦长为2.
为直径的圆截得的弦长为2.

练习册系列答案
相关题目
【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.