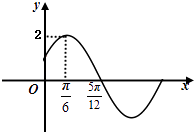
题目内容
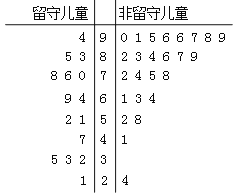
【题目】【2015高考湖北】如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
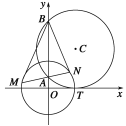
(1)圆C的标准方程为________.
(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:
①![]() =
=![]() ;②
;②![]() -
-![]() =2;
=2;
③![]() +
+![]() =2
=2![]() .
.
其中正确结论的序号是________(写出所有正确结论的序号).
【答案】(1)(x-1)2+(y-![]() )2=2 (2)①②③
)2=2 (2)①②③
【解析】(1)取AB的中点D,连接CD,则CD⊥AB.
由题意|AD|=|CD|=1,
故|AC|=![]() =
=![]() ,即圆C的半径为
,即圆C的半径为![]() .
.
又因为圆C与x轴相切于点T(1,0),所以圆心C的坐标为(1,![]() ),故圆C的标准方程为(x-1)2+(y-
),故圆C的标准方程为(x-1)2+(y-![]() )2=2.
)2=2.
(2)在(x-1)2+(y-![]() )2=2中,令x=0,得y=
)2=2中,令x=0,得y=![]() ±1,
±1,
故A(0,![]() -1),B(0,
-1),B(0,![]() +1).设M(x1,y1),N(x2,y2),
+1).设M(x1,y1),N(x2,y2),
当直线MN斜率不存在时,令M(0,-1),N(0,1),
则![]() =
=![]() =
=![]() -1,
-1,![]() =
=![]() =
=![]() -1.
-1.
∴![]() =
=![]() .
.
当直线MN斜率存在时,设直线MN的方程为y=kx+![]() -1,由
-1,由![]()
得(1+k2)x2+2(![]() -1)kx+2(1-
-1)kx+2(1-![]() )=0,
)=0,
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
kBM+kNB=![]() +
+![]()
=![]() +
+![]()
=![]() +
+![]() =-
=-![]() +2k
+2k
=-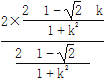 +2k=0,
+2k=0,
所以kBM=-kNB,所以∠MBA=∠NBA,BA是∠MBN的平分线.
由内角平分线定理得![]() =
=![]() ,即
,即![]() =
=![]() .
.
故![]() =
=![]() 恒成立.
恒成立.
当k=0时,可求得![]() =
=![]() -1,
-1,
故![]() =
=![]() -1为定值.
-1为定值.
所以![]() -
-![]() =
=![]() -(
-(![]() -1)=2,
-1)=2,
![]() +
+![]() =
=![]() +
+![]() -1=2
-1=2![]() .
.
故①②③都正确.

练习册系列答案
相关题目