题目内容
设函数f(x)=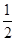 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0.
(1)当k>0时,判断f(x)在(0,+∞)上的单调性;
(2)讨论f(x)的极值点.
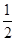 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0.(1)当k>0时,判断f(x)在(0,+∞)上的单调性;
(2)讨论f(x)的极值点.
(1)f(x)在(0,+∞)上单调递增
(2)x0是f(x)唯一的极小值点 见解析
(2)x0是f(x)唯一的极小值点 见解析
f′(x)=x+2+ .
.
(1)当k>0时,f′(x)=x+2+ >0在(0,+∞)恒成立,
>0在(0,+∞)恒成立,
所以f(x)在(0,+∞)上单调递增.
(2)函数f(x)的定义域为(0,+∞),
令f′(x)= =0,
=0,
得(x+1)2=1-k>(0+1)2=1,
所以当k>0时,f′(x)=0在(0,+∞)没有根,f(x)没有极值点;
当k<0时,f′(x)=0在(0,+∞)有唯一根x0=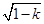 -1,
-1,
因为在(0,x0)上f′(x)<0,在(x0,+∞)上f′(x)>0,
所以x0是f(x)唯一的极小值点.
 .
.(1)当k>0时,f′(x)=x+2+
 >0在(0,+∞)恒成立,
>0在(0,+∞)恒成立,所以f(x)在(0,+∞)上单调递增.
(2)函数f(x)的定义域为(0,+∞),
令f′(x)=
 =0,
=0,得(x+1)2=1-k>(0+1)2=1,
所以当k>0时,f′(x)=0在(0,+∞)没有根,f(x)没有极值点;
当k<0时,f′(x)=0在(0,+∞)有唯一根x0=
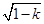 -1,
-1,因为在(0,x0)上f′(x)<0,在(x0,+∞)上f′(x)>0,
所以x0是f(x)唯一的极小值点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
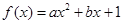 (
(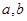 为实数,
为实数,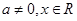 ),
),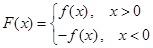 ,⑴若
,⑴若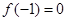 ,且函数
,且函数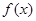 的值域为
的值域为 ,求
,求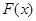 的表达式;
的表达式;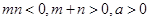 ,且函数
,且函数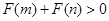 是否大0?
是否大0?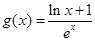 ,当
,当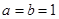 时,证明:对任意实数
时,证明:对任意实数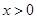 ,
,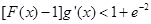 (其中
(其中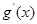 是
是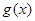 的导函数) .
的导函数) .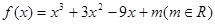 .
.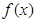 的极值(用含
的极值(用含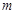 的式子表示);
的式子表示);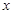 轴有3个不同交点,求
轴有3个不同交点,求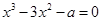 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.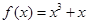 ,
,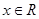 .若当
.若当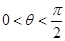 时,不等式
时,不等式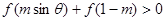 恒成立,则实数
恒成立,则实数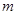 的取值范围是( )
的取值范围是( )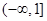
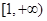
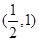
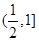
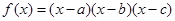 ,(
,(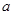 、
、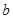 、
、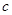 是两两不等的常数),则
是两两不等的常数),则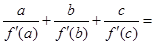 .
. ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.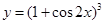 的导数。
的导数。