题目内容
(本题满分16分)
已知有穷数列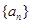 共有
共有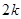 项(整数
项(整数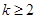 ),首项
),首项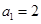 ,设该数列的前
,设该数列的前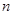 项和为
项和为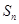 ,且
,且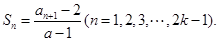 其中常数
其中常数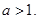 ⑴求
⑴求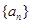 的通项公式;⑵若
的通项公式;⑵若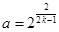 ,数列
,数列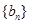 满足
满足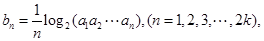
求证: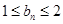 ;
;
⑶若⑵中数列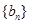 满足不等式:
满足不等式: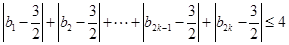 ,求
,求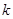 的最大值.
的最大值.
已知有穷数列
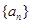 共有
共有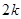 项(整数
项(整数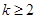 ),首项
),首项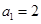 ,设该数列的前
,设该数列的前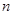 项和为
项和为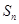 ,且
,且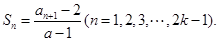 其中常数
其中常数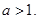 ⑴求
⑴求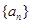 的通项公式;⑵若
的通项公式;⑵若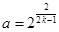 ,数列
,数列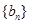 满足
满足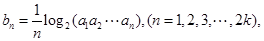
求证:
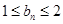 ;
;⑶若⑵中数列
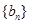 满足不等式:
满足不等式: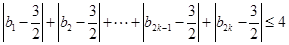 ,求
,求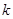 的最大值.
的最大值.⑴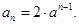 ⑵
⑵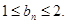 ⑶整数
⑶整数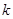 的最大值为7。
的最大值为7。
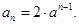 ⑵
⑵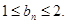 ⑶整数
⑶整数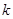 的最大值为7。
的最大值为7。试题分析:⑴
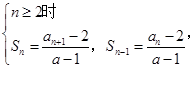
两式相减得
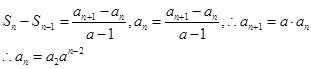
当
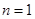 时
时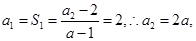 则,数列
则,数列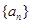 的通项公式为
的通项公式为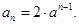
⑵把数列
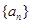 的通项公式代入数列
的通项公式代入数列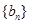 的通项公式,可得
的通项公式,可得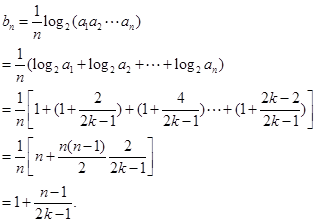
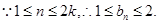
⑶数列
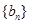 单调递增,且
单调递增,且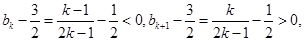
则原不等式左边即为
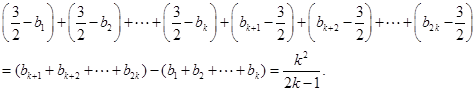
由
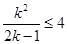 可得
可得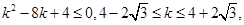 因此整数
因此整数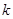 的最大值为7。
的最大值为7。点评:中档题,本解答从研究
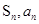 的关系入手,确定得到通项公式
的关系入手,确定得到通项公式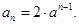 ,从而进一步明确
,从而进一步明确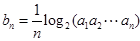 证明了
证明了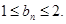 。“分组求和法”、“裂项相消法”、“错位相消法”是高考常常考到数列求和方法。
。“分组求和法”、“裂项相消法”、“错位相消法”是高考常常考到数列求和方法。
练习册系列答案
相关题目
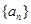 中,若
中,若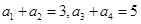 ,则
,则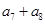 的和等于 ( )
的和等于 ( )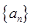 的前n项和为
的前n项和为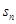 ,满足
,满足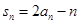
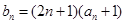 ,求数列
,求数列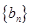 的前n项和
的前n项和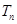 。
。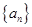 为等差数列,
为等差数列,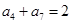 ,
,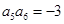 ,则
,则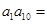 ( )
( )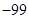
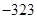
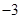
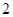
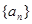 的前
的前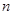 项和为
项和为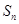 ,且
,且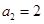 ,
,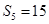 ,数列
,数列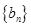 满足:
满足: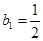 ,
,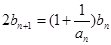 ,
,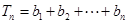 ,
,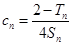 ,证明:
,证明:
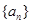 的通项公式
的通项公式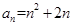 ,则数列
,则数列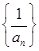 的前10项和为
的前10项和为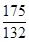

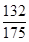
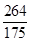
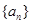 是公比为q的等比数列,其前n项的积为
是公比为q的等比数列,其前n项的积为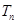 ,并且满足条件
,并且满足条件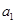 >1,
>1,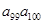 >1,
>1, 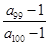 <0,给出下列结论:① 0<q<1;② T198<1;③
<0,给出下列结论:① 0<q<1;② T198<1;③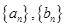 、的通项公式分别是
、的通项公式分别是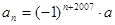 ,
,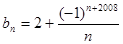 ,且
,且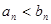 ,对任意
,对任意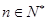 恒成立,则常数
恒成立,则常数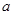 的取值范围是( )
的取值范围是( )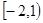
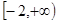
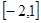
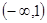
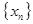 ,
,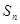 是
是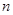 项和,且
项和,且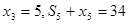 .
.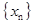 的通项公式;
的通项公式;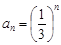 ,
,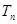 是
是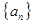 的前n项和,是否存在正数
的前n项和,是否存在正数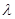 ,对任意正整数
,对任意正整数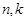 ,不等式
,不等式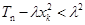 恒成立?若存在,求
恒成立?若存在,求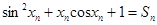 是否有解,说明理由;
是否有解,说明理由;