题目内容

设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1    (a＞b＞0)的左右焦点，
（1）设椭圆C上的点(
3
，
3
2
)到F1，F2两点距离之和等于4，写出椭圆C的方程和焦点坐标
（2）设K是（1）中所得椭圆上的动点，求线段KF1的中点B的轨迹方程
（3）设点P是椭圆C上的任意一点，过原点的直线L与椭圆相交于M，N两点，当直线PM，PN的斜率都存在，并记为kPM，KPN试探究kPM•KPN的值是否与点P及直线L有关，并证明你的结论．
（1）由于点(
3
，
3
2
)在椭圆上，
(
3
)2
a2
+
(
3
2
)2
b2
=1
2a=4，
椭圆C的方程为
x2
4
+
y2
3
=1
焦点坐标分别为（-1，0），（1，0）
（2）设KF1的中点为B（x，y）则点K（2x+1，2y）
把K的坐标代入椭圆
x2
4
+
y2
3
=1中得
(2x+1)2
4
+
(2y)2
3
=1
线段KF1的中点B的轨迹方程为(x+
1
2
)2+
y2
3
4
=1
（3）过原点的直线L与椭圆相交的两点M，N关于坐标原点对称
设M（x0，y0）N（-x0，-y0），p（x，y）
M，N，P在椭圆上，应满足椭圆方程，
得
x02
a2
+
y02
b2
=1，
x2
a2
+
y2
b2
=1
kPM=
y-y0
x-x0
，KPN=
y+y0
x+x0

kPM•KPN=
y-y0
x-x0
•
y+y0
x+x0
=
y2-y02
x2-x02
=-
b2
a2

kPM•KPN的值与点P及直线L无关
练习册系列答案
相关题目
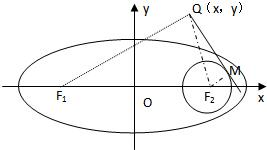精英家教网设F1，F2分别是椭圆C：
x2
6m2
+
y2
2m2
=1（m＞0）的左，右焦点．
（1）当P∈C，且
PF1
•
PF
2=0，|PF1|•|PF2|=8时，求椭圆C的左，右焦点F1、F2．
（2）F1、F2是（1）中的椭圆的左，右焦点，已知⊙F2的半径是1，过动点Q的作⊙F2切线QM，使得|QF1|=
2
|QM|（M是切点），如图．求动点Q的轨迹方程．
设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，且椭圆上一点P(1，
3
2
)到F1，F2两点距离之和等于4．
（Ⅰ）求此椭圆方程；
（Ⅱ）若直线l：y=kx+m（k≠0）与椭圆交于不同的两点M、N，且线段MN的垂直平分线过定点G(
1
8
，0)，求k的取值范围．
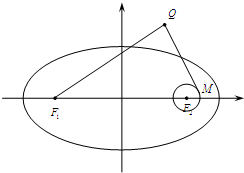精英家教网设F1、F2分别是椭圆C：
x2
6m2
+
y2
2m2
=1（m＞0）的左、右焦点．
（I）当p∈C，且
pF1
•
pF
2=0，|
pF1
|•|
pF
2|=4时，求椭圆C的左、右焦点F1、F2的坐标．
（II）F1、F2是（I）中的椭圆的左、右焦点，已知⊙F2的半径是1，过动点Q作的切线QM（M为切点），使得|QF1|=
2
|QM|，求动点Q的轨迹．
设F1，F2分别是椭圆C：
x2
a2
+
x2
b2
=1（a＞b＞0）的焦点，若椭圆C上存在点P，使线段PF1的垂直平分线过点F2，则椭圆离心率的取值范围是（　　）
（2013•肇庆二模）设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左右焦点．
（1）设椭圆C上的点(
2
2
，
3
2
)到F1，F2两点距离之和等于2
2
，写出椭圆C的方程；
（2）设过（1）中所得椭圆上的焦点F2且斜率为1的直线与其相交于A，B，求△ABF1的面积；
（3）设点P是椭圆C 上的任意一点，过原点的直线l与椭圆相交于M，N两点，当直线PM，PN的斜率都存在，并记为kPN，kPN试探究kPN•kPN的值是否与点P及直线l有关，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网