题目内容
已知函数
 .
.
(Ⅰ)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若 且对任意
且对任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: .
.
(Ⅰ)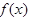 在
在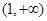 单调递增;在
单调递增;在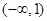 单调递减 4分
单调递减 4分
(Ⅱ)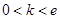 .
.
(Ⅲ)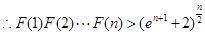 .
.
解析试题分析:(Ⅰ)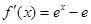 ,令
,令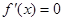 ,解得
,解得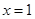
当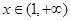 时,
时,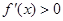 ,
,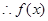 在
在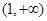 单调递增;
单调递增;
当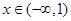 时,
时,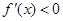 ,
,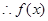 在
在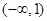 单调递减 4分
单调递减 4分
(Ⅱ) 为偶函数,
为偶函数,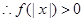 恒成立等价于
恒成立等价于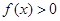 对
对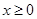 恒成立
恒成立
解法1:当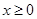 时,
时,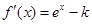 ,令
,令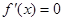 ,解得
,解得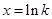
(1)当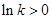 ,即
,即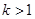 时,
时, 在
在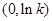 减,在
减,在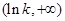 增
增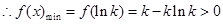 ,解得
,解得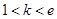 ,
,
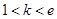
(2)当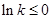 ,即
,即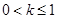 时,
时,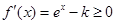 ,
,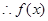 在
在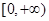 上单调递增,
上单调递增,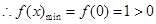 ,符合,
,符合,
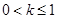
综上,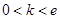 . 9分
. 9分
解法2: 等价于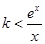 对
对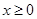 恒成立,
恒成立,
设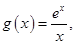 则
则 . 当
. 当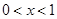 时,
时, 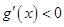 ;当
;当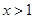 时,
时,  ;
;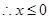 时,
时, 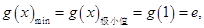
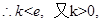
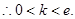
(Ⅲ)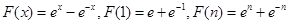
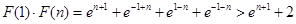
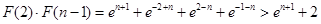
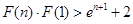
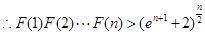 . 14分
. 14分
考点:应用导数研究函数的单调性,证明不等式恒。
点评:难题,本题属于导数应用中的基本问题,在某区间,导数值非负,函数为增函数,导数值非正,函数为减函数。不等式证明问题,往往通过构造函数,转化成了研究函数的最值,使问题得解。本题涉及不等式恒成立问题,通过研究函数的最值,解决了问题。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 满足
满足 ,
,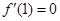 且
且 在
在 上恒成立.
上恒成立. 的值;
的值; ,解不等式
,解不等式 ;
; ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出实数
?若存在,请求出实数 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围 (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴. 是奇函数,且当
是奇函数,且当 时,
时, ,求
,求 时,
时,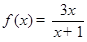 ,求
,求 在区间[2,5]上的最大值和最小值
在区间[2,5]上的最大值和最小值 上的奇函数f(x)在
上的奇函数f(x)在 上是减函数,若f(1-m)< f(m)
上是减函数,若f(1-m)< f(m) 的取值范围.
的取值范围. .
. 的单调区间; (2)若
的单调区间; (2)若 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
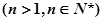
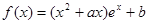 ,
,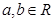 ,若函数
,若函数 在
在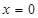 处的切线方程为
处的切线方程为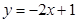 ,
,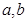 的值;
的值;