题目内容
【题目】已知直线
与直线
的交点为
，圆
.
（1）求过
的交点，且在两坐标轴上截距相等的直线方程；
（2）过点做圆
的切线，求切线方程.
【答案】（1）
或
；（2）
或
.
【解析】
（1）直线方程联立可求得
，分别讨论直线过原点和不过原点两种情况，从而求得直线方程；
（2）由圆的方程可确定圆心和半径；分别讨论过
的切线斜率存在和不存在两种情况，可知当斜率不存在时满足题意；当切线斜率存在时，利用圆心到直线距离等于半径可构造方程求得斜率，进而得到切线方程.
（1）由
得：，
①直线过原点，则方程为：；
②若直线不过原点，设方程为
，
将点
代入该方程得：
，故直线方程为.
综上所述：直线方程为或.
（2）圆
方程可整理为：
，则圆心
，半径
①当斜率不存在时，直线方程为，为圆的切线，满足题意；
②当切线斜率存在时，设方程为
，即
，
圆心到直线的距离
，解得：
，
切线方程为.
综上所述：切线方程为或.
练习册系列答案
相关题目
【题目】为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
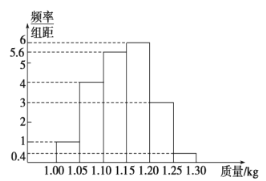
（1）在下面表格中填写相应的频率；
分组 | 频率 |
| |
| |
| |
| |
| |
|
（2）估计数据落在
中的概率；
（3）将上面捕捞的100条鱼分别作一记分组频率号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
