��Ŀ����
����Ŀ���ס��������̳���ͬһ����Ʒչ����������Թ������Ʒ�Ĺ˿������̳��Ľ����������£�
���̳����˿�ת����ͼ��ʾת�̣���ָ��ָ����Ӱ���֣�ͼ��������Ӱ���־�Ϊ���Σ���ÿ������Բ�ĽǾ�Ϊ![]() ���߽���Բ��ƣ���Ϊ�н���
���߽���Բ��ƣ���Ϊ�н���
���̳�����װ��4������4�������4������ĺ�����һ��������3����Щ�����ɫ����ȫ��ͬ���������������3����ͬ��ɫ����Ϊ�н���

�������ʣ��������Ʒ�Ĺ˿����ļ��̳��н��Ŀ����Դ�˵�����ɣ�
���������̳��������Ʒ�Ĺ˿���������ĸ���Ϊ![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
���𰸡���I���˿������̳��н��Ŀ����Դ�Щ�����ֲ��м������� ![]() .
.
�����������������������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() �����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�
�����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�![]() �����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ���������֪
�����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ���������֪![]() ��ȡֵΪ
��ȡֵΪ![]() ���ֱ������Ӧ�ĸ��ʣ��ɴ������
���ֱ������Ӧ�ĸ��ʣ��ɴ������![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�����������I����˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() ��ʳ�Ե�ȫ��������ɵ�����ΪԲ�̣����Ϊ
��ʳ�Ե�ȫ��������ɵ�����ΪԲ�̣����Ϊ![]() ��
��![]() ΪԲ�̵İ뾶������Ӱ��������Ϊ
ΪԲ�̵İ뾶������Ӱ��������Ϊ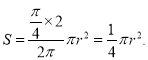
����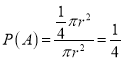
��˿�ȥ���̳�һ������3����ͬ��ɫ����Ϊ�¼�![]() ����һ�еȿ��ܵý����
����һ�еȿ��ܵý����![]() �֣�
�֣�
����![]() ��
��
��Ϊ![]() �����Թ˿������̳��н��Ŀ����Դ�Щ��
�����Թ˿������̳��н��Ŀ����Դ�Щ��
����������֪�� ![]() ��ȡֵΪ0,1,2,3.
��ȡֵΪ0,1,2,3.
��![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() ����ѧ����
����ѧ����![]() ��
��

