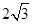题目内容
在 中,已知
中,已知 ,又
,又 的面积等于6.
的面积等于6.
(Ⅰ)求 的三边之长;
的三边之长;
(Ⅱ)设 是
是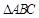 (含边界)内一点,
(含边界)内一点, 到三边
到三边 的距离分别为
的距离分别为 ,求
,求 的取值范围.
的取值范围.
 中,已知
中,已知 ,又
,又 的面积等于6.
的面积等于6.(Ⅰ)求
 的三边之长;
的三边之长;(Ⅱ)设
 是
是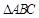 (含边界)内一点,
(含边界)内一点, 到三边
到三边 的距离分别为
的距离分别为 ,求
,求 的取值范围.
的取值范围.(Ⅰ)三边长分别为3,4,5.(Ⅱ)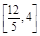 .
.
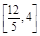 .
.试题分析:(Ⅰ)对条件
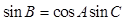 ,由正弦定理和余弦定理可以转化为只含边的等式,这个等式
,由正弦定理和余弦定理可以转化为只含边的等式,这个等式化简后为
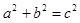 ,由此得
,由此得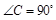 ,所以
,所以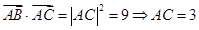 .再根据三角形的面积等于6可得BC=4,由勾股定理可得AB=5.
.再根据三角形的面积等于6可得BC=4,由勾股定理可得AB=5. (Ⅱ)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,设P点坐标为(x, y),则由点到直线的距离公式可将
 用点P的坐标表示出来,然后用线性规划可求出其取值范围.
用点P的坐标表示出来,然后用线性规划可求出其取值范围. 试题解析:(Ⅰ)法一、设三角形三内角A、B、C对应的三边分别为a, b, c,
∵
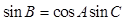 ,∴
,∴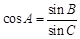 ,由正弦定理有
,由正弦定理有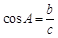 ,
,又由余弦定理有
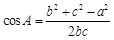 ,∴
,∴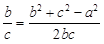 ,即
,即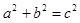 ,
,所以
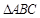 为Rt
为Rt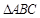 ,且
,且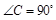 3分
3分所以
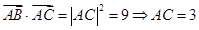
又
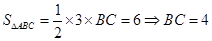 ,由勾股定理可得AB=5 6分
,由勾股定理可得AB=5 6分法二、设三角形三内角A、B、C对应的三边分别为a, b, c,
∵
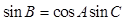 ,∴
,∴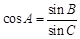 ,由正弦定理有
,由正弦定理有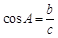 ,
,又由余弦定理有
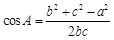 ,∴
,∴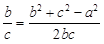 ,即
,即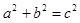 ,
,所以
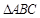 为Rt
为Rt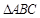 ,且
,且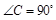 3分
3分又

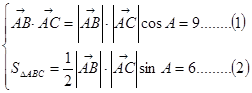
(1)÷(2),得
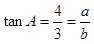 4分
4分令a="4k," b="3k" (k>0)
则
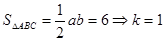 ∴三边长分别为3,4,5 6分
∴三边长分别为3,4,5 6分(Ⅱ)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,则A、B坐标为(3,0),(0,4),直线AB方程为
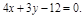
设P点坐标为(x, y),则由P到三边AB、BC、AB的距离为d1, d2和d3可知
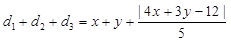 , 8分
, 8分且
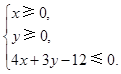 故
故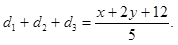 10分
10分令
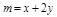 ,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是
,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是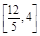 12分
12分
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 。
。 ,求
,求 的值。
的值。 的内角A、B、C所对的边为
的内角A、B、C所对的边为 ,
,  ,
,  ,且
,且 与
与 所成角为
所成角为 .
. 的取值范围.
的取值范围. ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记 ,
,
 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
 求
求 的值域;
的值域; 求
求 的值.
的值. 中,已知
中,已知 .
. 的值;
的值; ,
, ,求
,求 .
. b,且a>b,则∠B等于( )
b,且a>b,则∠B等于( )
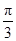


 的内角
的内角 满足
满足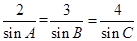 ,则
,则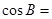 ( )
( )

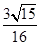

 的内角
的内角 对边分别为
对边分别为 且
且 则
则 =( )
=( )