题目内容
已知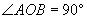 ,内有一动点P,
,内有一动点P,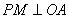 于M,
于M,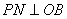 于N,且四边形PMON的面积等于4,今以O为原点,
于N,且四边形PMON的面积等于4,今以O为原点,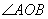 的平分线
的平分线 为极轴(如图),求动点P的轨迹方程。
为极轴(如图),求动点P的轨迹方程。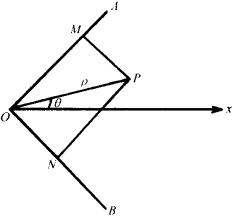
 ,内有一动点P,
,内有一动点P, 于M,
于M,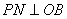 于N,且四边形PMON的面积等于4,今以O为原点,
于N,且四边形PMON的面积等于4,今以O为原点,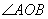 的平分线
的平分线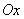 为极轴(如图),求动点P的轨迹方程。
为极轴(如图),求动点P的轨迹方程。

设P点坐标为( ,0),
,0),
∴ ,
, ,
,
故四边形PMON的面积



∴ 为
为 点极坐标为方程,
点极坐标为方程,
若化为直角坐标方程即 是双曲线右支。
是双曲线右支。
 ,0),
,0),∴
 ,
, ,
,故四边形PMON的面积




∴
 为
为 点极坐标为方程,
点极坐标为方程,若化为直角坐标方程即
 是双曲线右支。
是双曲线右支。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左、右焦点分别为F1、F2,短轴端点分别为A、B,且四边形F1AF2B是边长为2的正方形
的左、右焦点分别为F1、F2,短轴端点分别为A、B,且四边形F1AF2B是边长为2的正方形
 ,连结CM交椭圆于P,证明
,连结CM交椭圆于P,证明 为定值(O为坐标原点);
为定值(O为坐标原点);

 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。
 ,求a的取值范围。
,求a的取值范围。 的中心在原点,焦点在
的中心在原点,焦点在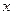 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为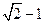 ,离心率为
,离心率为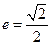 .
.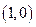 作直线
作直线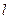 交
交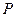 、
、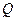 两点,试问:在
两点,试问:在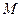 ,使
,使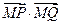 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点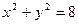 内有一点
内有一点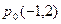 ,AB为过点
,AB为过点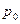 且倾斜角为α的弦,
且倾斜角为α的弦,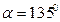 时,求AB的长;
时,求AB的长; 所在的平面
所在的平面 和四边形
和四边形 所在的平面
所在的平面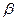 垂直,且
垂直,且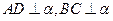 ,
,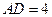 ,
,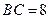 ,
,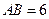 ,
,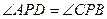 ,则点
,则点 在平面
在平面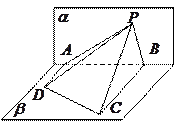
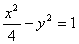 , 直线
, 直线 通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值
通过其右焦点F2,且与双曲线的右支交于A、B两点,将A、B与双曲线的左焦点F1连结起来,求|F1A|·|F1B|的最小值