题目内容
把边长为
的正方形ABCD沿对角线AC折成直二面角，折成直二面角后，在A，B，C，D四点所在的球面上，B与D两点之间的球面距离为（ ）
| 2 |
A、
| ||
| B、π | ||
C、
| ||
D、
|
分析：求解本题需要根据题意求解出题目中的角AOC的余弦，再代入求解，即可求出MN的两点距离．
解答：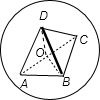
解：根据题意画出示意图，如图．
设AC的中点为O，则O点到四个点A，B，C，D的距离相等，
∴O是球的球心，半径R=OA=1，
且∠BOD=
，
B与D两点之间的球面距离为：
×1=
．
故选C．
解：根据题意画出示意图，如图．设AC的中点为O，则O点到四个点A，B，C，D的距离相等，
∴O是球的球心，半径R=OA=1，
且∠BOD=
| π |
| 2 |
B与D两点之间的球面距离为：
| π |
| 2 |
| π |
| 2 |
故选C．
点评：本题考查学生的空间想象能力，以及学生对球面上的点的距离求解，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
C.2 D.