题目内容
ABCD是边长为2的正方形，以BD为棱把它折成直二面角A-BD-C，E是CD的中点，则异面直线AE、BC的距离为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
分析：先证出CE是异面直线AE与BC的公垂线段，其长为所求．进而求得CE即可．
解答：解：取BD中点O，
∵E为DC的中点，
∴OE∥BC
∵BC⊥CD
∴OE⊥CD，
∵直二面角A-BD-C，
∴AO⊥面BDC，∴AO⊥DC
∴CD⊥平面AOE
∴CD⊥AE
∴CE是异面直线AE、BC的公垂线，
CE=
DC=1
故选D
∵E为DC的中点，
∴OE∥BC
∵BC⊥CD
∴OE⊥CD，
∵直二面角A-BD-C，
∴AO⊥面BDC，∴AO⊥DC
∴CD⊥平面AOE
∴CD⊥AE
∴CE是异面直线AE、BC的公垂线，
CE=
| 1 |
| 2 |
故选D
点评：本题主要考查了点，线，面得距离计算．当涉及异面直线的距离时，找到公垂线是解题的关键．
练习册系列答案
相关题目
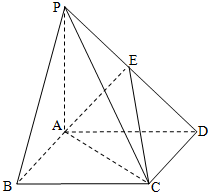设四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥面ABCD，PA=AB，E为PD的中点．
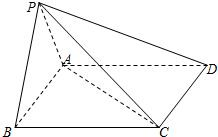如图，在四棱锥P-ABCD中，平面PAB⊥平面ABCD，底面ABCD是边长为2的正方形，△PAB为等边三角形．
如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．
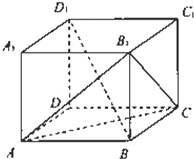如图，在长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，BB=
（2008•崇明县一模）（理科）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA⊥底面ABCD，PA=4，M为PA的中点，N为BC的中点．