题目内容
15.已知二次函数f(x)=ax2+bx+1和g(x)=$\frac{bx-1}{{a}^{2}x+2b}$;(1)f(x)为偶函数,试判断g(x)的奇偶性;
(2)若方程g(x)=x有两个不相等的实根,当a>0时判断f(x)在(-1,1)上的单调性;
(3)若方程g(x)=x的两实根为x1,x2,f(x)=0的两根为x3,x4,求使x1<x2<x3<x4成立的a的取值范围.
分析 (1)根据f(x)为偶函数容易得到b=0,从而得到g(x)=$-\frac{1}{{a}^{2}x}$,从而可判断出g(x)为奇函数;
(2)由方程g(x)=x可以得到a2x2+bx+1=0,而根据该方程有两个不等实根便可得到b2>4a2,由a>0,便可得出b>2a,或b<-2a,进一步可以求出$-\frac{b}{2a}$的范围,从而可判断出f(x)在(-1,1)上的单调性;
(3)先得到$\left\{\begin{array}{l}{{a}^{2}{x}^{2}+bx+1=0}\\{a{x}^{2}+bx+1=0}\end{array}\right.$,可设α为x1,x2中的一个数,从而可以得到$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{(α-{x}_{3})(α-{x}_{4})>0}\end{array}\right.$,而根据${x}_{3}+{x}_{4}=-\frac{b}{a},{x}_{1}{x}_{2}=\frac{1}{a}$便可得到$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{{α}^{2}+\frac{b}{a}α+\frac{1}{a}>0}\end{array}\right.$.这时可讨论a,从而可以化简${α}^{2}+\frac{b}{a}α+\frac{1}{a}>0$:a>0时会得到a-a2>0,可解出0<a<1;a<0时会得到a-a2<0,可以解出a<0,这样便可求出a的取值范围.
解答 解:(1)f(x)为偶函数;
∴f(-x)=f(x);
即ax2-bx+1=ax2+bx+1;
∴b=0;
∴$g(x)=-\frac{1}{{a}^{2}x}$;
g(x)的定义域为{x|x≠0},且g(-x)=g(x);
∴g(x)为奇函数;
(2)由g(x)=x得,$\frac{bx-1}{{a}^{2}x+2b}=x$;
整理得,a2x2+bx+1=0,该方程有两个不等实根;
∴△=b2-4a2>0,a>0;
∴b>2a,或b<-2a;
∴$-\frac{b}{2a}<-1,或-\frac{b}{2a}>1$;
f(x)的对称轴为$x=-\frac{b}{2a}$;
∴b>2a时,f(x)在(-1,1)上单调递增,b<-2a时,f(x)在(-1,1)上单调递减;
(3)由$\left\{\begin{array}{l}{g(x)=x}\\{f(x)=0}\end{array}\right.$得,$\left\{\begin{array}{l}{{a}^{2}{x}^{2}+bx+1=0}\\{a{x}^{2}+bx+1=0}\end{array}\right.$;
设α为x1,x2中的一个数,则:$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{(α-{x}_{3})(α-{x}_{4})>0}\end{array}\right.$;
∵${x}_{3}+{x}_{4}=-\frac{b}{a},{x}_{3}{x}_{4}=\frac{1}{a}$;
∴$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{{α}^{2}+\frac{b}{a}α+\frac{1}{a}>0}\end{array}\right.$;
①若a>0,则$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{a{α}^{2}+bα+1>0}\end{array}\right.$;
两式联立可得(a-a2)α2>0;
∴a-a2>0;
∴0<a<1;
②若a<0,则$\left\{\begin{array}{l}{{a}^{2}{α}^{2}+bα+1=0}\\{a{α}^{2}+bα+1<0}\end{array}\right.$;
联立两式得(a-a2)α2<0;
∴a-a2<0;
∴a>1,或a<0;
∴a<0;
∴综上得,a的取值范围为(-∞,0)∪(0,1).
点评 考查偶函数、奇函数的定义及判断过程,一元二次方程实根的个数和判别式△的关系,以及二次函数的对称轴,二次函数的单调性及单调区间,韦达定理,解一元二次不等式.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案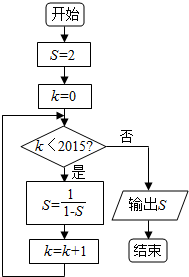
| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 命题“若x>1,则x2>1”的否命题 | |
| B. | 命题“若x>y,则|x|>y”的逆命题 | |
| C. | 若k<5,则两椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$与$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$有不同的焦点 | |
| D. | 命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
| A. | y=-x2 | B. | y=ex-e-x | C. | y=ln(|x|+1) | D. | y=x•sinx+cosx |
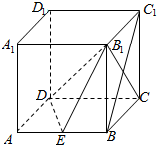 如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.
如图,在正方体ABCD-A1B1C1D1的棱长为a,E为棱AB上的一动点.