题目内容
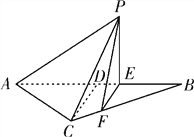
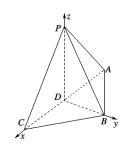
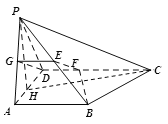
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() △
△![]() 为等边三角形,
为等边三角形, ![]() 是
是![]() 上的点,且
上的点,且![]() .
.
(1)求![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.
【答案】(1)![]() (2)PB中点
(2)PB中点
【解析】试题分析:(1)分别利用等腰三角形的三线合一和线面垂直的性质得到线线垂直,进而利用线面垂直的判定定理证明线面垂直,作出线面角,再利用直角三角形进行求解;(2)先猜出该点位置,再利用利用线面垂直的判定定理进行证明.
试题解析:(1)取AD中点H,PD=PA, 所以![]() ,因为AB
,因为AB![]() 平面PAD,且PH
平面PAD,且PH![]() 平面PAD,
平面PAD,
所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() ∠PCH是PC和平面ABCD所成的角.
∠PCH是PC和平面ABCD所成的角.
不妨令AB=2 ,CH=![]()
在△![]()
(2)线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.
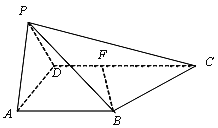
理由如下:如图,分别取![]() 的中点G、E,则
的中点G、E,则![]() , 由
, 由![]() , 所以
, 所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,故
为平行四边形,故![]() .
.
因为AB![]() 平面PAD,所以
平面PAD,所以![]() ,因此,
,因此, ![]() ,因为
,因为![]() 为
为![]() 的中点,且
的中点,且![]() ,
, ![]() ,因此
,因此![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.

 互动英语系列答案
互动英语系列答案【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
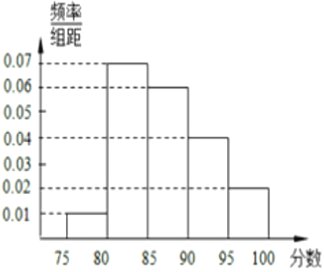
【题目】某高校在今年的自主招生考试成绩中随机抽取 100 名考生的笔试成绩,分为 5 组制出频率分布直方图如图所示.
组号 | 分组 | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 35 | 0.35 |
3 |
|
|
|
4 |
|
|
|
5 |
| 10 | 0.1 |
(1)求![]() 的值.
的值.
(2)该校决定在成绩较好的 、4、5 组用分层抽样抽取 6 名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,从抽到 6 名学生中再随机抽取 2 名被甲考官面试,求这 2 名学生来自同一组的概率.