题目内容
【题目】设平面直角坐标系xOy中,曲线G:y= ![]() +
+ ![]() x﹣a2(x∈R),a为常数.
x﹣a2(x∈R),a为常数.
(1)若a≠0,曲线G的图象与两坐标轴有三个交点,求经过这三个交点的圆C的一般方程;
(2)在(1)的条件下,求圆心C所在曲线的轨迹方程;
(3)若a=0,已知点M(0,3),在y轴上存在定点N(异于点M)满足:对于圆C上任一点P,都有 ![]() 为一常数,试求所有满足条件的点N的坐标及该常数.
为一常数,试求所有满足条件的点N的坐标及该常数.
【答案】
(1)解:令x=0,得曲线与y轴的交点是(0,﹣a2),
令y=0,则 ![]() +
+ ![]() x﹣a2=0,解得x=﹣2a或x=a,
x﹣a2=0,解得x=﹣2a或x=a,
∴曲线与x轴的交点是(﹣2a,0),(a,0).
设圆的一般方程为x2+y2+Dx+Ey+F=0,则 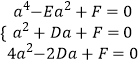 ,
,
解得D=a,E=a2﹣2,F=﹣2a2,
∴圆的一般方程为x2+y2+ax+(a2﹣2)y﹣2a2=0;
(2)解:由(1)可得C(﹣ ![]() ,
, ![]() )
)
设C(x,y),则x=﹣ ![]() ,y=
,y= ![]() ,消去a,得到y=1﹣2x2,
,消去a,得到y=1﹣2x2,
∵a≠0,
∴x≠0,
∴圆心C所在曲线的轨迹方程为y=1﹣2x2(x≠0)
(3)解:若a=0,圆C的方程为x2+(y﹣1)2=1,
令x=0,得到圆C与y轴交于点(0,0),(0,2)
由题意设y轴上的点N(0,t)(t≠3),
当P与圆C的交点为(0,2)时, ![]() =
= ![]() ,
,
当P与圆C的交点为(0,0)时, ![]() =
= ![]() ,
,
由题意, ![]() =
= ![]() ,∴t=
,∴t= ![]() (t=3舍去)
(t=3舍去)
下面证明点N(0, ![]() ),对于圆C上任一点P,都有
),对于圆C上任一点P,都有 ![]() 为一常数
为一常数
设P(x,y),则x2+(y﹣1)2=1,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴在y轴上存在定点N(0, ![]() ),满足:对于圆C上任一点P,都有
),满足:对于圆C上任一点P,都有 ![]() 为一常数
为一常数 ![]()
【解析】(1)求出曲线G的图象与两坐标轴有三个交点,利用待定系数法求经过这三个交点的圆C的一般方程;(2)由(1)可得C(﹣ ![]() ,
, ![]() ),消去a,求圆心C所在曲线的轨迹方程;(3)令x=0,得到圆C与y轴交于点(0,0),(0,2),由此求出点N(0,
),消去a,求圆心C所在曲线的轨迹方程;(3)令x=0,得到圆C与y轴交于点(0,0),(0,2),由此求出点N(0, ![]() ),对于圆C上任一点P,都有
),对于圆C上任一点P,都有 ![]() 为一常数,再进行证明即可.
为一常数,再进行证明即可.
【考点精析】本题主要考查了圆的一般方程的相关知识点,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |