��Ŀ����
����Ŀ����ͼ������ƽ��ֱ������ϵxOy��x���ڵ�ƽ���ϣ�y�ᴹֱ�ڵ�ƽ�棬��λ����Ϊ1ǧ�ף�ij��λ������ԭ�㣮��֪�ڵ������Ĺ켣�ڷ���y=kx-![]() ��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
��1����k=2ʱ�����ڵ���̣�
��2�����ڵ������̣�
��3�����ڵ�һ������һ������������С��������и߶�Ϊ3.2ǧ�ף��������ĺ�����a����������ʱ���ڵ���������������˵�����ɣ�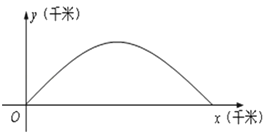
���𰸡��⣺��1����k=2��y=kx-![]() ���ɵã�y=2x-
���ɵã�y=2x-![]() ��y=0���ɵ�x=0��x=8��
��y=0���ɵ�x=0��x=8��
�ڵ����Ϊ��8ǧ�ף�
��2���� y=kx��![]() ��1+k2��x2��k��0������y=0���� kx��
��1+k2��x2��k��0������y=0���� kx��![]() ��1+k2��x2=0��
��1+k2��x2=0��
��ʵ���������������֪x��0��k��0��
��x=![]() =
=![]() ��
��![]() =10�����ҽ���k=1ʱȡ�Ⱥţ�
=10�����ҽ���k=1ʱȡ�Ⱥţ�
���ڵ���������10ǧ�ף�
��3����a��0�����ڵ����Ի���Ŀ��ȼ��ڴ��� k��0��ʹka��![]() ��1+k2��a2��3.2������
��1+k2��a2��3.2������
������k�ķ���a2k2��20ak+a2+64=0��������
��Τ�ﶨ����������֮�ʹ���0������֮������0��
��ֻ���=400a2��4a2��a2+64����0����a��6��
��ʱ��k=![]() ��0��
��0��
�൱a������6ʱ���ڵ����Ի���Ŀ�꣮
����������1��ͨ��k=2������������ʽ�������ö��κ��������̣�
��2�����ڵ�����Ŀ��ʱ�ĺ���������ֵ����һԪ���η��̸����б�ʽ��⼴�ɣ�
��3���ڵ����Ի���Ŀ��ȼ��ڴ��� k��0��ʹka��![]() ��1+k2��a2��3.2������ת��Ϊ����k�ķ���a2k2��20ak+a2+64=0�������������б�ʽ����⼴�ɣ�
��1+k2��a2��3.2������ת��Ϊ����k�ķ���a2k2��20ak+a2+64=0�������������б�ʽ����⼴�ɣ�

 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�