题目内容
18.四棱锥P-ABCD中,CD∥AB,CD=2AB,E为PC中点,R为CD中点.(1)求证:平面BER∥面PAD;
(2)若BE=AD=4,PA=4$\sqrt{3}$,求异面直线BE与DA所成角的大小.
分析 (1)由已知得四边形ABRD是平行四边形,从而BR∥AD,由此能证明平面BER∥面PAD.
(2)由BR∥AD,且BR=AD=4,得∠EBR是异面直线BE与DA所成角(或所成角的补角),连结AC,交BR于点G,则G是AC中点,连结EG,由此利用余弦定理能求出异面直线BE与DA所成角的大小.
解答 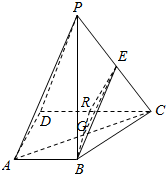 (1)证明:∵四棱锥P-ABCD中,CD∥AB,CD=2AB,E为PC中点,R为CD中点,
(1)证明:∵四棱锥P-ABCD中,CD∥AB,CD=2AB,E为PC中点,R为CD中点,
∴ER∥PD,AB$\underset{∥}{=}$DR,∴四边形ABRD是平行四边形,
∴BR∥AD,
∵ER∩BR=R,AD∩PD=D,AD?平面ADP,PD?平面ADP,BR?平面BRE,ER?平面BRE,
∴平面BER∥面PAD.
(2)解:∵四边形ABRD是平行四边形,
∴BR∥AD,且BR=AD=4,
∴∠EBR是异面直线BE与DA所成角(或所成角的补角),
连结AC,交BR于点G,则G是AC中点,连结EG,
则EG=$\frac{1}{2}PA=2\sqrt{3}$,BG=2,
在△BEG中,cos∠EBR=$\frac{{4}^{2}+4-12}{2×4×2}$=$\frac{1}{2}$,
∴∠EBR的大小为60°,∴异面直线BE与DA所成角的大小为60.
点评 本题考查面面平行的证明,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
9.对定义在R上的两个函数f(x)=ex-e-x和g(x)=sinx,则( )
| A. | f(x)g(x)是奇函数 | B. | f(g(x))是奇函数 | C. | g(f(x))是偶函数 | D. | |f(x)|g(x)偶函数 |
13.函数y=-x2、y=$\frac{1}{x}$、y=2x+1、y=$\sqrt{x}$在x=1附近(△x很小时),平均变化率最大的一个是( )
| A. | y=-x2 | B. | y=$\frac{1}{x}$ | C. | y=2x+1 | D. | y=$\sqrt{x}$ |
3.已知集合A={-1,1},B={∅,{-1},{1},{-1,1}},则A与B的关系是( )
| A. | A⊆B | B. | A∈B | C. | A与B无关系 | D. | A?B |
 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.