题目内容
8.在二项式($\frac{1}{2}$+2x)n的展开式中:(1)若第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;
(2)若所有项的二项式系数和等于4096,求展开式中系数最大的项.
分析 (1)由第5项,第6项与第7项的二项式系数成等差数列求得n的值,可得展开式中二项式系数最大的项.
(2)求得n=12,再利用二项展开式的通项公式,求得展开式中系数最大的项.
解答 解:(1)因为2${C}_{n}^{5}$=${C}_{n}^{4}$+${C}_{n}^{6}$,所以 n=7,或 n=14.
当n=7时,二项式系数最大的项为 T4=$\frac{35}{2}$x3,T5=70x4.
当n=14时,二项式系数最大的项为T8=${C}_{17}^{4}$•x7.
(2)因为2n=4096,所以n=12.
又因为 $\left\{\begin{array}{l}{{C}_{12}^{k}{•(\frac{1}{2})}^{12-k}{•2}^{k}{≥C}_{12}^{k-1}{•(\frac{1}{2})}^{13-k}{•2}^{k-1}}\\{{C}_{12}^{k}{•(\frac{1}{2})}^{12-k}{•2}^{k}{≥C}_{12}^{k+1}{•(\frac{1}{2})}^{11-k}{•2}^{k+1}}\end{array}\right.$,所以k=10,所以展开式中系数最大的项为T11=33•29•x10.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
16.过点C(-1,1)和D(1,3),圆心在x轴上的圆的方程是( )
| A. | x2+(y-2)2=10 | B. | x2+(y+2)2=10 | C. | (x-2)2+y2=10 | D. | (x+2)2+y2=10 |
17.如图各网格是单位正方形,粗线所表示的图形为某几何体的三视图.则该几何体的体积为( )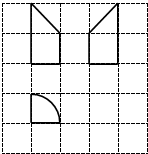

| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |