题目内容
7. 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P、Q分别是棱DD1、CC1的中点.(1)画出面D1BQ与面ABCD的交线,简述画法及确定交线的依据.(2)求证:平面D1BQ∥平面PAO.
分析 (1)延长D1Q与DC,交于点M,连接BM.得BM即为面D1BQ与面ABCD的交线.由已知能推导出M在面D1BQ与面ABCD的交线上,B也在面D1BQ与面ABCD的交线上,从而得到BM即为面D1BQ与面ABCD的交线.
(2)连接PQ、BD,四边形PABQ为平行四边形,从而AP∥BQ,进而BQ∥面AOP,同理可证D1B∥面AOP,由此能证明面BQD1∥面AOP.
解答 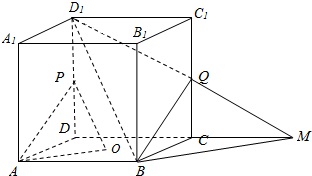 (1)解:作法:延长D1Q与DC,交于点M,连接BM.得BM即为面D1BQ与面ABCD的交线…(2分)
(1)解:作法:延长D1Q与DC,交于点M,连接BM.得BM即为面D1BQ与面ABCD的交线…(2分)
理由如下:
由作法可知,M∈直线D1Q,
又∵直线D1Q?面D1BQ,∴M∈面D1BQ,
同理可证M∈面ABCD,
则M在面D1BQ与面ABCD的交线上,
又∵B∈面D1BQ,且B∈面ABCD,
则B也在面D1BQ与面ABCD的交线上,…(4分)
且面D1BQ与面ABCD有且只有一条交线,
则BM即为面D1BQ与面ABCD的交线.…(5分)
(2)证明:连接PQ、BD,由已知得四边形PABQ为平行四边形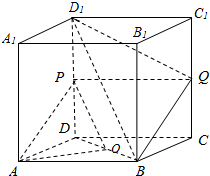
∴AP∥BQ,∵AP?面AOP,BQ?面AOP,
∴BQ∥面AOP,…(8分)
同理可证D1B∥面AOP,
又∵BQ∩D1B=B,BQ?面BQD1,BD1?面BQD1,
∴面BQD1∥面AOP.…(10分)
点评 本题考查两平面交线的作法及证明,考查两平面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
16.过点C(-1,1)和D(1,3),圆心在x轴上的圆的方程是( )
| A. | x2+(y-2)2=10 | B. | x2+(y+2)2=10 | C. | (x-2)2+y2=10 | D. | (x+2)2+y2=10 |
17.如图各网格是单位正方形,粗线所表示的图形为某几何体的三视图.则该几何体的体积为( )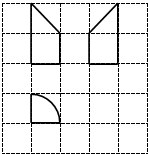

| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
 如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数:
如图,边长为1正方形ABCD中,分别在边BC、AD上各取一点M与N,下面用随机模拟的方法计算|MN|>1.1的概率.利用计算机中的随机函数产生两个0~1之间的随机实数x,y,设BM=x,AN=y,则可确定M、N点的位置,进而计算线段MN的长度.设x,y组成数对(x,y),经随机模拟产生了20组随机数: