题目内容
设函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,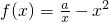 (a为实数).
(a为实数).
(1)若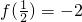 ,求a的值;
,求a的值;
(2)当x∈(0,1]时,求f(x)的解析式;
(3)当a>2时,试判断f(x)在(0,1]上的单调性,并证明你的结论.
解:(1)∵f(x)是奇函数,∴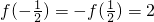 ∴
∴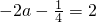 ,∴
,∴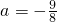 .
.
(2)设x∈(0,1],则-x∈[-1,0),∴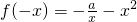 ,∵f (x)是奇函数,
,∵f (x)是奇函数,
∴f(-x)=f(x),∴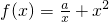 .
.
(3)当a>2时,f(x)在(0,1]上单调递减
证明:设x1,x2∈(0,1]且x1<x1,
则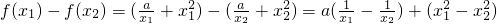
=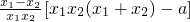 ,∵x1,x2∈(0,1],
,∵x1,x2∈(0,1],
∴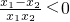 ,x1x2•(x1+x2)∈(0,2),
,x1x2•(x1+x2)∈(0,2),
当a>2时,x1x2•(x1+x2)-a<0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴当a>2时,f(x)在(0,1]上单调递减.
分析:(1)根据f(x)是奇函数,可得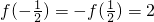 ,解方程求得a的值.
,解方程求得a的值.
(2)设x∈(0,1],则-x∈[-1,0),故有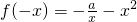 ,根据奇函数的定义解出f (x).
,根据奇函数的定义解出f (x).
(3)当a>2时,f(x)在(0,1]上单调递减,设x1,x2∈(0,1]且x1<x1,可证得f(x1)-f(x2)>0,
可得结论成立.
点评:本题考查奇函数的定义,函数单调性的定义和证明方法,求函数的解析式是解题的难点.
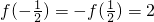 ∴
∴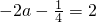 ,∴
,∴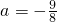 .
.(2)设x∈(0,1],则-x∈[-1,0),∴
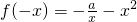 ,∵f (x)是奇函数,
,∵f (x)是奇函数,∴f(-x)=f(x),∴
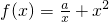 .
.(3)当a>2时,f(x)在(0,1]上单调递减
证明:设x1,x2∈(0,1]且x1<x1,
则
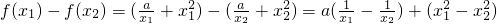
=
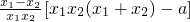 ,∵x1,x2∈(0,1],
,∵x1,x2∈(0,1],∴
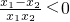 ,x1x2•(x1+x2)∈(0,2),
,x1x2•(x1+x2)∈(0,2),当a>2时,x1x2•(x1+x2)-a<0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴当a>2时,f(x)在(0,1]上单调递减.
分析:(1)根据f(x)是奇函数,可得
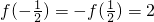 ,解方程求得a的值.
,解方程求得a的值.(2)设x∈(0,1],则-x∈[-1,0),故有
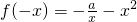 ,根据奇函数的定义解出f (x).
,根据奇函数的定义解出f (x).(3)当a>2时,f(x)在(0,1]上单调递减,设x1,x2∈(0,1]且x1<x1,可证得f(x1)-f(x2)>0,
可得结论成立.
点评:本题考查奇函数的定义,函数单调性的定义和证明方法,求函数的解析式是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目