题目内容
(本小题满分16分)![]()
![]() 点,点A1(x1,0),A2(x
点,点A1(x1,0),A2(x![]() ,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x
,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x![]() - x
- x![]() 是常数,并求数列{ x
是常数,并求数列{ x![]() }的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.
}的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.
(I)![]() (II)
(II)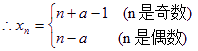 (3)
(3)![]()
解析:
: ![]() …2分
…2分
![]() 相减,得x
相减,得x![]() -x
-x![]() =2
=2
∴x![]() ,x
,x![]() ,x
,x![]() ,…,x
,…,x![]() ,…成等差数列;x
,…成等差数列;x![]() ,x
,x![]() ,x
,x![]() ,…,x
,…,x![]() ,…成等差数列,4分
,…成等差数列,4分
∴x![]() = x
= x![]() +(n-1)·2=2n+a-2,x
+(n-1)·2=2n+a-2,x![]() = x
= x![]() +(n-1)·2=(2-a)+(n-1)·2=2n-a
+(n-1)·2=(2-a)+(n-1)·2=2n-a
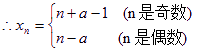 …7分
…7分
(3)当n奇数时,An(n+a-1,0),An+1(n+1-a,0),所以 | AnAn+1 | =2(1-a);
当n是偶数时,An(n-a,0),An+1(n+a,0),所以| AnAn-1 | =2a …10分
![]()
要使等腰三角形AnBnAn+1为直角三角形,必需且只需| AnAn-1 | =2| BnCn | .
![]()
![]() ……14分
……14分
![]() …15分
…15分
![]() …16分
…16分
点评:复习时把握数列的概念,记住一些常用的结论,灵活的使用,注重对数列结合不等式等综合问题的解决。数列与不等式均是高考的必考内容,而将数列与不等式结合成大题则是高考中的一个难点问题,复习中应强化这方面的训练.

练习册系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.