题目内容
已知关于x的二次方程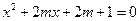
(1)若方程有两根,其中一根在区间 内,另一根在区间
内,另一根在区间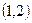 内,求m的取值范围
内,求m的取值范围
(2)若方程两根均在区间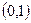 内,求m的取值范围
内,求m的取值范围
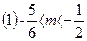
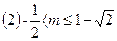
解析

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
题目内容
已知关于x的二次方程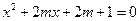
(1)若方程有两根,其中一根在区间 内,另一根在区间
内,另一根在区间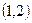 内,求m的取值范围
内,求m的取值范围
(2)若方程两根均在区间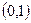 内,求m的取值范围
内,求m的取值范围
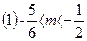
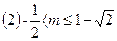
解析

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案