题目内容
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
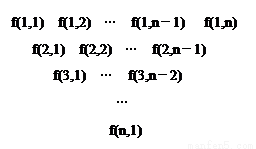 Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当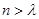 时,都有Sn >m.
时,都有Sn >m.
【答案】
(1)数表中第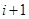 行的数依次所组成数列的通项为
行的数依次所组成数列的通项为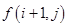 ,则由题意可得
,则由题意可得
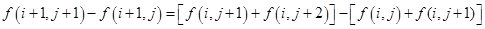
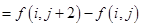
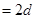 (其中
(其中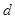 为第
为第 行数所组成的数列的公差) .
行数所组成的数列的公差) .
(2)  .
.
(3)  .
.
【解析】(1)数表中第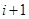 行的数依次所组成数列的通项为
行的数依次所组成数列的通项为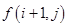 ,则由题意可得
,则由题意可得
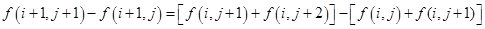
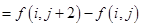
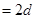 (其中
(其中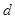 为第
为第 行数所组成的数列的公差) .
行数所组成的数列的公差) .
(2)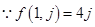 ,
,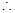 第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列.
第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列.
设第 行的数公差为
行的数公差为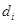 ,则
,则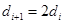 ,则
,则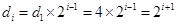
所以
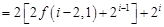
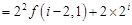
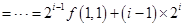
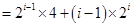
 .
.
(3)由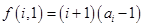 ,可得
,可得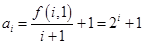
所以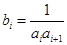
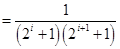 =
=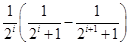
令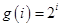 ,则
,则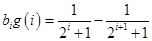 ,所以
,所以 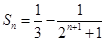
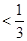
要使得 ,即
,即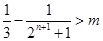 ,只要
,只要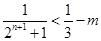 =
=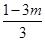 ,
,
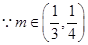 ,
,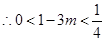 ,所以只要
,所以只要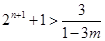 ,
,
即只要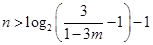 ,所以可以令
,所以可以令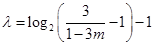
则当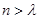 时,都有
时,都有 .所以适合题设的一个函数为
.所以适合题设的一个函数为 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.