题目内容
在△ABC中,已知sinC=2sin(B+C)cosB,那么△ABC一定是( )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
B
解析试题分析:由内角和是π,据诱导公式消去C,再由两角和与差的公式变换整理,观察整理的结果判断出△ABC一定是等腰三角形. 解:∵sinC=2sin(B+C)cosB,∴sin(A+B)=2sinAcosB,∴sinAcosB+cosAsinB=2sinAcosB,∴sinAcosB-cosAsinB=0,∴sin(A-B)=0,∴A-B=0,即A=B,故△ABC一定是等腰三角形,故应选B
考点:两角与差的正弦公式
点评:本题考查三角函数的两角与差的正弦公式,利用此公式变换出A-B=0.从本题的变换中可以体会出三角变换的灵活性

练习册系列答案
相关题目
在△ABC中,一定成立的等式是( )
A. | B. |
C. | D. |
在已知 ABC的内角
ABC的内角 的对边
的对边 若a=csinA则
若a=csinA则 的最大值为( )
的最大值为( )
A. | B.1 | C. | D. |
已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为 ( )
| A.9 | B.18 | C.9 | D.18 |
 的内角
的内角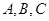 所对的边分别为
所对的边分别为 ,
, ,
, ,
, ,则此三角形( )
,则此三角形( )
| A.一定是锐角三角形 |
| B.一定是直角三角形 |
| C.一定是钝角三角形 |
| D.可能是钝角三角形,也可能是锐角三角形 |
在 中,内角
中,内角 ,
, ,
, 所对的边分别是
所对的边分别是 ,已知
,已知 ,
, ,则
,则 ( )
( )
A. | B. |
C. | D. |
在 中,若
中,若 ,则
,则 ( )
( )
A.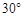 | B. | C. | D. |
在△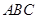 中,若
中,若 ,则△
,则△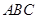 的形状是( )
的形状是( )
| A.钝角三角形 | B.直角三角形 | C.锐角三角形 | D.不能确定 |
 的内角A、B、C满足
的内角A、B、C满足 ,则
,则 =( )
=( ) B.
B.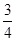 C.
C. D.
D.