Question

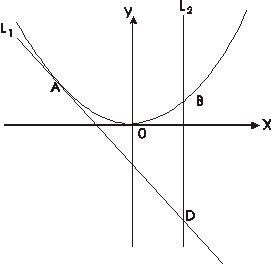已知点A（-1，2）是抛物线C：y=2x²上的点，直线l₁过点A，且与抛物线C相切，直线l₂：x=a（a≠-1）交抛物线C于点B，交直线l₁于点D．
（1）求直线l₁的方程；
（2）设△BAD的面积为S₁，求|BD|及S₁的值；
（3）设由抛物线C，直线l₁，l₂所围成的图形的面积为S₂，求证：S₁：S₂的值为与a无关的常数．

Answer 1

分析：（1）由y=2x²，得y′=4x．当x=-1时，y'=-4．由此能求出l₁的方程．
（2）由

y=2x2 x=a

，得：B点坐标为（a，2a²）．由

x=a 4x+y+12=0

，得D点坐标（a，-4a-2）．点A到直线BD的距离为|a+1|．由此能求出|BD|及S₁的值．
（3）当a＞-1时，S₁=（a+1）³，S₂=∫_-1^a[2x²-（-4x-2）]dx=∫_-1^a（2x²+4x+2）dx=

2

3

(a+1)3．S₁：S₂=

3

2

．当a＜-1时，S₁=-（a+1）³，S₂=∫_a^-1[2x²-（-4x-2）]dx=∫_a^-1（2x²+4x+2）dx=-

2

3

(a+1)3．S₁：S₂=

3

2

，综上可知S₁：S₂的值为与a无关的常数，这常数是

3

2

．

解答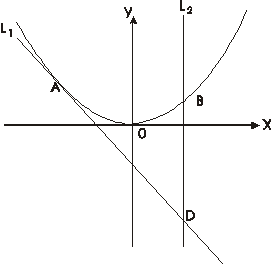：解：（1）由y=2x²，得y′=4x．当x=-1时，y'=-4．（2分）
∴l₁的方程为y-2=-4（x+1），即y=-4x-2．（3分）
（2）由

y=2x2 x=a

，得：B点坐标为（a，2a²）．（4分）
由

x=a 4x+y+2=0

，得D点坐标（a，-4a-2）．（5分）
∴点A到直线BD的距离为|a+1|．（6分）
|BD|=2a²+4a+2=2（a+1）²
∴S₁=|a+1|³．（7分）
（3）当a＞-1时，S₁=（a+1）³，（8分）
S₂=∫_-1^a[2x²-（-4x-2）]dx
=∫_-1^a（2x²+4x+2）dx
=(

2

3

x3+2x2+2x)

|

a -1

=

2

3

(a+1)3．（9分）
∴S₁：S₂=

3

2

．（11分）
当a＜-1时，S₁=-（a+1）³
S₂=∫_a^-1[2x²-（-4x-2）]dx
=∫_a^-1（2x²+4x+2）dx
=-

2

3

(a+1)3．（13分）
∴S₁：S₂=

3

2

，综上可知S₁：S₂的值为与a无关的常数，这常数是

3

2

．（14分）

点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与双曲线的相关知识，解题时要注意双曲线的性质、导数、定积分的灵活运用，合理地进行等价转化．