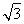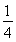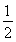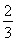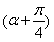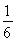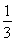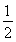题目内容
如图所示,角A为钝角,且sin A=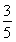 ,点P,Q分别是在角A的两边上不同于点A的动点.
,点P,Q分别是在角A的两边上不同于点A的动点.

(1)若AP=5,PQ=3 ,求AQ的长;
,求AQ的长;
(2)若∠APQ=α,∠AQP=β,且cos α= ,求sin(2α+β)的值.
,求sin(2α+β)的值.
(1)2.(2)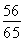
【解析】∵角A是钝角,sin A=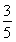 ,∴cos A=-
,∴cos A=-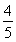 .
.
(1)在△APQ中,由余弦定理得PQ2=AP2+AQ2-2AP·AQcos A,所以AQ2+8AQ-20=0,
解得AQ=2或-10(舍去负值),所以AQ=2.
(2)由cos α=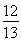 ,得sin α=
,得sin α=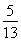 ,
,
在△APQ中,α+β+A=π,
得sin(α+β)=sin(π-A)=sin A=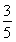 ,cos(α+β)=-cos A=
,cos(α+β)=-cos A=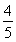 ,
,
∴sin(2α+β)=sin[α+(α+β)]=sin αcos(α+β)+cos αsin(α+β)=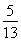 ×
×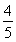 +
+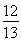 ×
×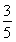 =
=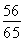 .
.

练习册系列答案
相关题目