题目内容
【题目】已知![]() 为定义在R上的奇函数,当
为定义在R上的奇函数,当![]() 时,
时,![]() 为二次函数,且满足
为二次函数,且满足![]() ,
,![]() 在
在![]() 上的两个零点为
上的两个零点为![]() 和
和![]() .
.
(1)求函数![]() 在R上的解析式;
在R上的解析式;
(2)作出![]() 的图象,并根据图象讨论关于
的图象,并根据图象讨论关于![]() 的方程
的方程![]()
![]() 根的个数.
根的个数.
【答案】(1)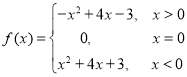 ;(2)当
;(2)当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;当
个根;当![]() 或
或![]() 时,方程有
时,方程有![]() 个根; 当
个根; 当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;当
个根;当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
【解析】
试题分析:(1)当![]() 时,根据
时,根据![]() 在
在![]() 上的两个零点为
上的两个零点为![]() 和
和![]() ,设函数为两根式即
,设函数为两根式即![]() ,
,![]() ,所以解得
,所以解得![]() ,当
,当![]() 时,
时,![]() ,∵
,∵![]() 为
为![]() 上的奇函数,∴
上的奇函数,∴![]() ,求得解析式为
,求得解析式为![]() ,因为奇函数
,因为奇函数![]() ,可得函数解析式;(2)关于
,可得函数解析式;(2)关于![]() 的方程
的方程![]()
![]() 根的个数,即函数
根的个数,即函数![]() 与
与![]() 交点的个数,作出
交点的个数,作出![]() 的图象可得
的图象可得
试题分析:(1)由题意,当![]() 时,设
时,设![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]()
(注:设![]() 一样给分)
一样给分)
当![]() 时,
时,![]() ,∵
,∵![]() 为
为![]() 上的奇函数,∴
上的奇函数,∴![]() ,
,
∴![]()
即![]() 时,
时,![]()
当![]() 时,由
时,由![]() 得:
得:![]()
所以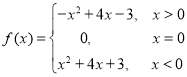 .
.
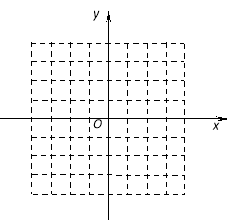
(2)作出![]() 的图象(如图所示)
的图象(如图所示)

(注:![]() 的点或两空心点不标注扣1分,
的点或两空心点不标注扣1分,
不要重复扣分)
由![]() 得:
得:![]() ,在图中作
,在图中作![]() ,
,
根据交点讨论方程的根:
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 时,方程有
时,方程有![]() 个根.
个根.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
, ![]() ,
,