题目内容
20.若数列{an}的前n项和Sn=n2-2n,求通项公式an.分析 由前n项和求得首项,由an=Sn-Sn-1得到n≥2时的通项公式,验证首项后得答案.
解答 解:∵Sn=n2-2n,
∴${a}_{1}={S}_{1}={1}^{2}-2×1=-1$;
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}={n}^{2}-2n-[(n-1)^{2}-2(n-1)]$
=2n-3.
验证n=1时,上式成立.
∴an=2n-3.
点评 本题考查由数列的前n项和求数列的通项公式,是基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.如图,由曲线y=x2和直线y=$\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)的面积是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
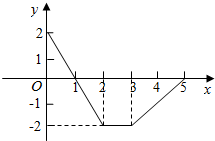 已知y=f(x)的图象如图所示.
已知y=f(x)的图象如图所示.