题目内容
11.已知△ABC的三个内角满足sinA:sinB:sinC=5:11:13,则△ABC是( )| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
分析 由条件利用正弦定理可得a:b:c=5:11:13,C为最大角.再由余弦定理可得cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$<0,可得C为钝角,从而得出结论.
解答 解:由△ABC的三个内角满足sinA:sinB:sinC=5:11:13,利用正弦定理可得a:b:c=5:11:13,
设a=5k,则b=11k,c=13k,故C为最大角.
由余弦定理可得cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{2{5k}^{2}+12{1k}^{2}-16{9k}^{2}}{11{0k}^{2}}$=-$\frac{23}{110}$<0,
可得C为钝角,故△ABC是钝角三角形,
故选:D.
点评 本题主要考查正弦定理和余弦定理的应用,属于基础题.

练习册系列答案
相关题目
2.已知函数$f(x)=\left\{\begin{array}{l}lo{g_2}x+2,x>0\\{3^x},x≤0\end{array}\right.$,则$f[f(\frac{1}{8})]$的值( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -3 | D. | $-\frac{1}{3}$ |
19.已知数列{an}满足a1=2,an+1=$\frac{{1+{a_n}}}{{1-{a_n}}}$,则a15等于( )
| A. | 2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
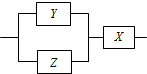 如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.
如图,用X、Y、Z这3类不同的元件连接成系统N,每个元件是否正常工作不受其它元件的影响,已知元件X、Y、Z正常工作的概率依次为0.8、0.7、0.9,则系统N正常工作的概率是0.776.