题目内容
2．已知函数$f（x）=\left\{\begin{array}{l}lo{g_2}x+2，x＞0\\{3^x}，x≤0\end{array}\right.$，则$f[f（\frac{1}{8}）]$的值（ ）| A． | 3 | B． | $\frac{1}{3}$ | C． | -3 | D． | $-\frac{1}{3}$ |
分析 根据分段函数的表达式，代入进行求解即可．
解答 解：f（$\frac{1}{8}$）=$lo{g}_{2}\frac{1}{8}$+2=-3+2=-1，
f（-1）=${3}^{-1}=\frac{1}{3}$，
即$f[f（\frac{1}{8}）]$=f（-1）=$\frac{1}{3}$，
故选：B
点评 本题主要考查函数值的计算，比较基础．
练习册系列答案
相关题目
12．已知等腰△OAB中|OA|=|OB|=2，且$|{\overrightarrow{{O}{A}}+\overrightarrow{{O}{B}}}|≥\frac{{\sqrt{3}}}{3}|{\overrightarrow{{A}{B}}}|$，那么$\overrightarrow{{O}{A}}•\overrightarrow{{O}{B}}$的取值范围是：（ ）
| A． | [-2，4） | B． | （-2，4） | C． | （-4，2） | D． | （-4，2] |
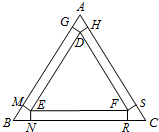如图：在边长为6米的等边△ABC钢板内，作一个△DEF，使得△DEF的三边到△ABC所对应的三边之间的距离均x（0＜x＜$\frac{2}{3}$$\sqrt{3}$）米，过点D分别向AB，AC边作垂线，垂足依次为G，H；过点E分别向AB，BC边作垂线，垂足依次为M，N；过点F分别向BC，AC边作垂线，垂足依次为R，S．接着在△ABC的三个内角处，分别沿DG，DH、EM，EN、FR，FS进行切割，割去的三个全等的小四边形分别为AGDH、BMEN、CRFS．然后把矩形GDEM、NEFR、SFDH分别沿DE、EF、FD向上垂直翻折，并对翻折后的钢板进行无缝焊接（注：切割和无缝焊接过程中的损耗和费用忽略不计），从而构成一个无盖的正三棱柱蓄水池．
7．若点P（x，y）的坐标x，y满足约束条件：$\left\{\begin{array}{l}x+y-6≤0\\ x-y+1≥0\\ x≥1\\ y≥1\end{array}\right.$，则$\frac{3x-4y}{5}$的最大值为（ ）
| A． | $-\frac{1}{5}$ | B． | -1 | C． | $\frac{11}{5}$ | D． | 11 |
11．已知△ABC的三个内角满足sinA：sinB：sinC=5：11：13，则△ABC是（ ）
| A． | 等腰三角形 | B． | 锐角三角形 | C． | 直角三角形 | D． | 钝角三角形 |