Question

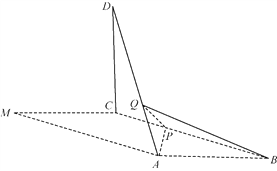
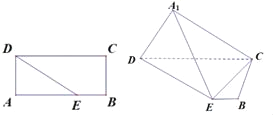
【题目】如图（1）在矩形ABCD中，AB＝5，AD＝2，点E在线段AB上，且BE＝1，将△ADE沿DE折起到△A1DE的位置，使得平面A1DE⊥平面BCDE，如图（2）．

（1）求证：CE⊥平面A1DE；

（2）求证：A1D⊥A1C；

（3）线段A1C上是否存在一点F，使得BF∥平面A1DE？说明理由．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）存在，为五等分点靠近点.

【解析】

（1）在两面垂直的前提下，垂直交线则垂直另一平面；

（2）通过计算利用勾股定理得证；

（3）需作出辅助平面，利用两面平行后，一个平面内的直线平行另一平面，得到点．

（1）证明：∵如图（1）在矩形ABCD中，

AB＝5，AD＝2，

点E在线段AB上，且BE＝1，

∴，

，

CD＝5，

∴，

∴CE⊥DE，

∵平面A1DE⊥平面BCDE，

∴CE⊥平面A1DE．

（2）由题意得A1D＝AD＝2，

A1E＝AE＝4，

，且CE⊥A1E，

∴A1C＝，

∴，

∴A1D⊥A1C．

（3）取CD上点M，使DM＝1＝BE，

又DM∥BE，

∴DMBE为平行四边形，

∴BM∥DE，

∴BM∥平面A1DE，

在△A1DC内，作MF∥A1D交A1C与F，

则MF∥平面A1DE，

∴平面FMB∥平面A1DE，

∴BF∥平面A1DE，

故存在点F（A1C的五等分点靠近点A1），

使得BF∥平面A1DE．