题目内容
已知等差数列 满足
满足 .
.
(1)求 的通项公式;
的通项公式;
(2)求 的前
的前 项和
项和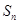 ;
;
(3)若 成等比数列,求
成等比数列,求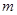 的值.
的值.
 满足
满足 .
.(1)求
 的通项公式;
的通项公式;(2)求
 的前
的前 项和
项和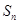 ;
;(3)若
 成等比数列,求
成等比数列,求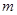 的值.
的值.(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
试题分析:
(1)法一:根据数列是等差数列,采用特殊值带入
 ,求出首项和公差,得通项公式;法二:根据等差数列的通项公式展开
,求出首项和公差,得通项公式;法二:根据等差数列的通项公式展开 的左侧,则其左侧含有
的左侧,则其左侧含有 ,根据等式相等关系,可得
,根据等式相等关系,可得 ,从而得到通项公式.
,从而得到通项公式.(2)利用等差数列前
 项和公式以及(1)中的结论直接求即可.
项和公式以及(1)中的结论直接求即可.(3)根据(1)中结论,以及等比中项可解该问.
(1)解法一:设
 的公差为
的公差为 , 因为
, 因为 ,
,所以有
 ,两式相减得到,
,两式相减得到, ,即
,即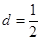
代入得到

所以

解法二:设
 的公差为
的公差为 ,
,则

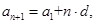
所以

所以有
 对
对 成立,
成立,所以有
 ,解得
,解得
所以

(2) 因为
 所以
所以
(3)因为
 成等比数列,所以
成等比数列,所以
即

解得

 (舍掉) ,所以
(舍掉) ,所以 …
… 项和公式,等比中项.
项和公式,等比中项.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若项数为
,若项数为 的数列
的数列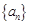 满足:对任意的
满足:对任意的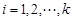 ,均有
,均有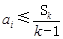 (其中
(其中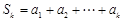 ),则称数列
),则称数列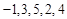 和
和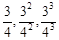 是否是“Γ数列”,并说明理由;
是否是“Γ数列”,并说明理由; 对
对 是公差为
是公差为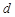 的无穷项等差数列,若对任意的正整数
的无穷项等差数列,若对任意的正整数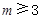 ,
,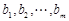
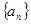 中,若
中,若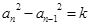 (
(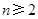 ,
,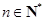 ,
,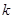 为常数),则称
为常数),则称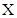 数列.
数列.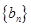 是
是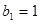 ,
,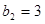 ,写出所有满足条件的数列
,写出所有满足条件的数列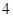 项;
项;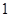 或
或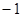 ;
;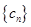 满足
满足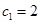 ,
,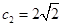 ,
,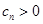 ,设数列
,设数列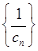 的前
的前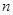 项和为
项和为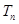 .是否存在
.是否存在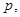
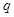 ,使不等式
,使不等式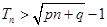 对一切
对一切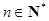 都成立?若存在,求出
都成立?若存在,求出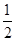 ,
,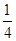 ,…,
,…,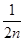 ,….是( )
,….是( )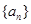 中,
中,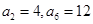 ,则
,则



 的前
的前 项和为
项和为 ,且
,且 ,则
,则 为( )
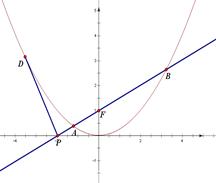
为( )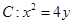 ,直线
,直线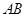 过抛物线
过抛物线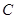 的焦点
的焦点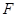 ,交
,交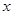 轴于点
轴于点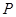 .
.
 ;
; (异于原点),
(异于原点),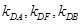 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;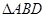 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.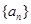 中,
中,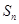 是它的前n项之和,且
是它的前n项之和,且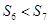 ,
,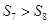 ,则:
,则: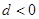 ; ②
; ②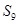 一定小于
一定小于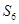 ;
;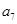 是各项中最大的一项; ④
是各项中最大的一项; ④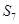 一定是
一定是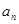 }的前
}的前 项和
项和 ,则
,则 的值为 ( )
的值为 ( ) 


