题目内容
(2011•昌平区二模)如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
(1)求证:BD1∥平面A1DE;
(2)求证:D1E⊥A1D;
(3)在线段AB上是否存在点M,使二面角D1-MC-D的大小为
?若存在,求出AM的长;若不存在,请说明理由.
(1)求证:BD1∥平面A1DE;
(2)求证:D1E⊥A1D;
(3)在线段AB上是否存在点M,使二面角D1-MC-D的大小为
| π | 6 |
分析:(1)O是AD1的中点,连接OE,由中位线定理可得EO∥BD1,再由线面平行的判定定理可得BD1∥平面A1DE;
(2)由正方形AA1D1D与矩形ABCD所在平面互相垂直,根据面面垂直的性质定理可得AB⊥平面ADD1A1,进而线线面垂直的性质定理得到AB⊥A1D,结合A1D⊥AD1及线面垂直的判定定理,可得A1D⊥平面AD1E,进而D1E⊥A1D;
(3)以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,设M(1,y0,0)(0≤y0≤2),分别求出平面D1MC的法向量和平面MCD的一个法向量,根据二面角D1-MC-D的大小为
,结合向量夹角公式,构造关于m的方程,解方程可得M占的坐标,进而求出AM长.
(2)由正方形AA1D1D与矩形ABCD所在平面互相垂直,根据面面垂直的性质定理可得AB⊥平面ADD1A1,进而线线面垂直的性质定理得到AB⊥A1D,结合A1D⊥AD1及线面垂直的判定定理,可得A1D⊥平面AD1E,进而D1E⊥A1D;
(3)以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,设M(1,y0,0)(0≤y0≤2),分别求出平面D1MC的法向量和平面MCD的一个法向量,根据二面角D1-MC-D的大小为
| π |
| 6 |
解答: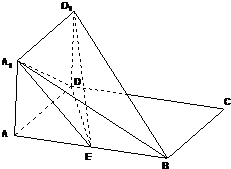 证明:(1)四边形ADD1A1为正方形,O是AD1的中点,点E为AB的中点,连接OE.
证明:(1)四边形ADD1A1为正方形,O是AD1的中点,点E为AB的中点,连接OE.
∴EO为△ABD1的中位线∴EO∥BD1…(2分)
又∵BD1?平面A1DE,OB?平面A1DE∴BD1∥平面A1DE …(4分)
(2)由已知可得:AE⊥平面ADD1A1,A1D?平面ADD1A1
∴AE⊥A1D,
又∵A1D⊥AD1,AE∩AD1=A
∴A1D⊥平面AD1E,D1E?平面AD1E
∴A1D⊥D1E….(4分)
解:(3)由题意可得:D1D⊥平面ABCD,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D(0,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1),
设M(1,y0,0)(0≤y0≤2),∵
=(-1,2-y0,0),
=(0,2,-1)
设平面D1MC的法向量为n1=(x,y,z)则
,得
取D1MC是平面D1MC的一个法向量,而平面MCD的一个法向量为n2=(0,0,1)要使二面角D1-MC-D的大小为
,
而cos
=|cos<n1,n2>|=
=
=
解得:y0=2-
(0≤y0≤2),当AM=2-
时,二面角D1-MC-D的大小为
…(6分)
 证明:(1)四边形ADD1A1为正方形,O是AD1的中点,点E为AB的中点,连接OE.
证明:(1)四边形ADD1A1为正方形,O是AD1的中点,点E为AB的中点,连接OE.∴EO为△ABD1的中位线∴EO∥BD1…(2分)
又∵BD1?平面A1DE,OB?平面A1DE∴BD1∥平面A1DE …(4分)
(2)由已知可得:AE⊥平面ADD1A1,A1D?平面ADD1A1
∴AE⊥A1D,
又∵A1D⊥AD1,AE∩AD1=A
∴A1D⊥平面AD1E,D1E?平面AD1E
∴A1D⊥D1E….(4分)
解:(3)由题意可得:D1D⊥平面ABCD,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D(0,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1),
设M(1,y0,0)(0≤y0≤2),∵
| MC |
| D1C |
设平面D1MC的法向量为n1=(x,y,z)则
|
|
取D1MC是平面D1MC的一个法向量,而平面MCD的一个法向量为n2=(0,0,1)要使二面角D1-MC-D的大小为
| π |
| 6 |
而cos
| π |
| 6 |
| |n1•n2| |
| |n1|•|n2| |
| 2 | ||
|
| ||
| 2 |
解得:y0=2-
| ||
| 3 |
| ||
| 3 |
| π |
| 6 |
点评:本题考查的知识点是用空间向量求平面间的夹角,空间中直线与直线之间的位置关系,直线与平面平行的判定,其中(1)的关键是证得EO∥BD1,(2)的关键是熟练掌握线线垂直,线面垂直与面面垂直之间的相互转化,(3)的关键是设出M点坐标,求出两个半平面的法向量,然后结合向量夹角公式构造方程.

练习册系列答案
相关题目