Question

（2011•昌平区二模）若不等式组

x+2y-5≤0 x≥1 y≥1

表示的平面区域是一个三角形，则此三角形的面积是

1

；若x，y满足上述约束条件，则z=x-y的最大值是

2

．

Answer 1

分析：先根据约束条件画出可行域，然后求出区域的面积即可，设z=x-y，再利用z的几何意义求最值，只需求出直线z=x-y过可行域内的点A（3，1）时，从而得到z=x-y的最大值即可．

解答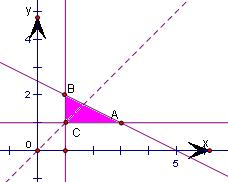：解：先画出约束条件

x+2y-5≤0 x≥1 y≥1

所表示的区域，如图．
所围成图形是一个三角形，其中：A （3，1），B（1，2），C（1，1）．
∴三角形ABC的面积为S=

1

2

×AC×BC=

1

2

×2×1=1；
由图可知，当直线z=x-y过点A（3，1）时，z最大，
即最优解为A（3，1），
故Z_max=3-1=2．
故答案为：1，2．

点评：本题主要考查了用平面区域二元一次不等式组和围成区域的面积，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．