题目内容
(本小题满分14分)已知函数 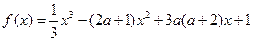 ,
,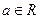 .
.
(1)当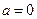 时,求曲线
时,求曲线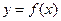 在点(3,
在点(3,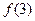 )处的切线方程;
)处的切线方程;
(2)当函数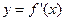 在
在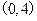 上有唯一的零点时,求实数
上有唯一的零点时,求实数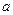 的取值范围.
的取值范围.
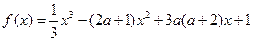 ,
,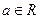 .
.(1)当
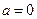 时,求曲线
时,求曲线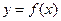 在点(3,
在点(3,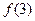 )处的切线方程;
)处的切线方程;(2)当函数
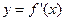 在
在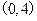 上有唯一的零点时,求实数
上有唯一的零点时,求实数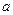 的取值范围.
的取值范围.解:(1)当a=0时,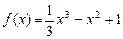 ,
,
∴f(3)=1, ∵f'(x)=x2-2x ………3分
曲线在点(3,1)处的切线的斜率k=f'(3)="3 " ………4分
∴所求的切线方程为y-1=3(x-3),即y="3x-8 " ………6分
(2)∵f'(x)=x2-2(2a+1)x+3a(a+2)="(x-3a)(x-a-2) " ∴x1=3a,x2=a+2
①当x1=x2时,3a=a+2,解得a=1,这时x1=x2=3,函数y=f'(x)在(0,4)上
有唯一的零点,故a=1为所求;………7分
②当x1>x2时,即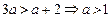 ,这时x1>x2>3,
,这时x1>x2>3,
又函数y=f'(x)在(0,4)上有唯一的零点,
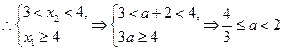 ..........10分
..........10分
③当x1<x2时,即a<1,这时x1<x2<3
又函数y=f'(x)在(0,4)上有唯一的零点,
∴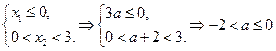 ………13分
………13分
综上得当函数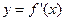 在
在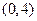 上有唯一的零点时,
上有唯一的零点时,
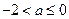 或
或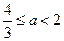 或
或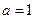 . ………14分
. ………14分
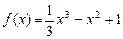 ,
,∴f(3)=1, ∵f'(x)=x2-2x ………3分
曲线在点(3,1)处的切线的斜率k=f'(3)="3 " ………4分
∴所求的切线方程为y-1=3(x-3),即y="3x-8 " ………6分
(2)∵f'(x)=x2-2(2a+1)x+3a(a+2)="(x-3a)(x-a-2) " ∴x1=3a,x2=a+2
①当x1=x2时,3a=a+2,解得a=1,这时x1=x2=3,函数y=f'(x)在(0,4)上
有唯一的零点,故a=1为所求;………7分
②当x1>x2时,即
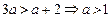 ,这时x1>x2>3,
,这时x1>x2>3,又函数y=f'(x)在(0,4)上有唯一的零点,
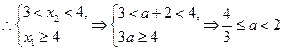 ..........10分
..........10分③当x1<x2时,即a<1,这时x1<x2<3
又函数y=f'(x)在(0,4)上有唯一的零点,
∴
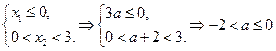 ………13分
………13分综上得当函数
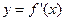 在
在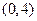 上有唯一的零点时,
上有唯一的零点时,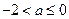 或
或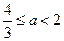 或
或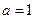 . ………14分
. ………14分略

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
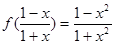 ,则
,则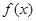 的解析式可能为( )
的解析式可能为( )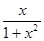
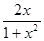

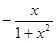
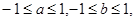 则关于
则关于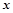 的方程
的方程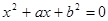 有实根的概率是( )
有实根的概率是( )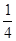
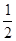
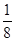
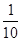
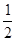 的
的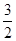 }
}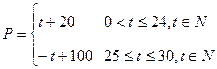
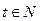 ),
),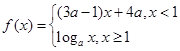 满足:对任意实数
满足:对任意实数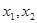 ,当
,当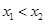 时,总有
时,总有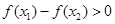 ,那么实数
,那么实数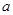 的取值范围是 ( )
的取值范围是 ( )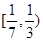
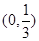
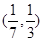
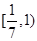
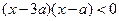 ,
,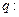 实数
实数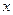 满足
满足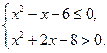 .
.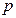 的
的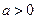 时,若
时,若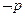 是
是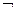
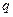 的充分不必要条件,求实数
的充分不必要条件,求实数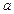 的取值范围.
的取值范围.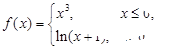 若f(2-x2)>f(x),则实数x的取值范围( )
若f(2-x2)>f(x),则实数x的取值范围( )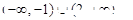

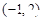
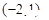
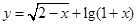 的定义域为( )
的定义域为( )