题目内容
12.在平面直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y=16{t}^{2}-9}\end{array}\right.$(t为参数),倾斜角等于$\frac{2π}{3}$的直线l经过P,在以原点O为极点,x轴正半轴为极轴的极坐标系中,点P的极坐标为(1,$\frac{π}{2}$)(1)求点P的直角坐标;
(2)设l与曲线C交于A、B两点,求|PA|•|PB|的值.
分析 (1)根据x=ρcosθ、y=ρsinθ可得点P的直角坐标;
(2)利用参数的几何意义,即可求|PA|•|PB|.
解答 解:(1)点P的极坐标为(1,$\frac{π}{2}$),直角坐标为(0,1)
(2)倾斜角等于$\frac{2π}{3}$的直线l经过P,参数方程为$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$,
曲线C的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y=16{t}^{2}-9}\end{array}\right.$,普通方程为y=4x2-9,
代入可得t2-$\frac{\sqrt{3}}{2}$t-10=0,
∵点P的坐标为(0,1),
∴|PA|•|PB|=-10.
点评 本小题主要考查参数方程、极坐标方程等基础知识,考查参数的几何意义,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
17.参数方程$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=-1+2co{s}^{2}θ}\end{array}\right.$(θ为参数)化为普通方程是( )
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
2.“光盘行动”倡导厉行节约,反对铺张浪费,带动大家珍惜粮食,吃光盘子中的食物,得到从中央到民众的支持,为了解某地响应“光盘行动”的实际情况,某校几位同学组成研究性学习小组,从某社区[25,55]岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
(Ⅰ)求a,b的值,并估计本社区[25,55]岁的人群中“光盘族”所占比例;
(Ⅱ)从年龄段在[35,40)与[40,45)的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
(i)已知选取2人中1人来自[35,40)中的前提下,求另一人来自年龄段[40,45)中的概率;
(ii)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
| 组数 | 分组 | 频数 | 频率 | “光盘族”占本组比例 |
| 第1组 | [25,30) | 50 | 0.05 | 30% |
| 第2组 | [30,35) | 100 | 0.10 | 30% |
| 第3组 | [35,40) | 150 | 0.15 | 40% |
| 第4组 | [40,45) | 200 | 0.20 | 50% |
| 第5组 | [45,50) | a | b | 65% |
| 第6组 | [50,55) | 200 | 0.20 | 60% |
(Ⅱ)从年龄段在[35,40)与[40,45)的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
(i)已知选取2人中1人来自[35,40)中的前提下,求另一人来自年龄段[40,45)中的概率;
(ii)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
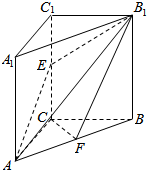 已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,
已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,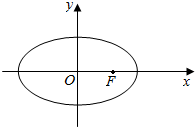 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)