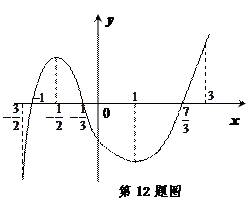
题目内容
(本小题满分13分
已知函数 ,
,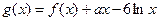 ,其中
,其中 R
R
(Ⅰ)讨论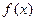 的单调性
的单调性
(Ⅱ)若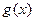 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围
的取值范围
(Ⅲ)设函数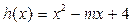 , 当
, 当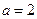 时,若
时,若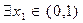 ,
,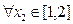 ,总有
,总有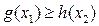 成立,求实数
成立,求实数 的取值范围
的取值范围
已知函数
 ,
,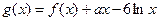 ,其中
,其中 R
R (Ⅰ)讨论
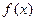 的单调性
的单调性(Ⅱ)若
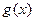 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围
的取值范围(Ⅲ)设函数
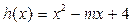 , 当
, 当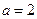 时,若
时,若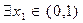 ,
,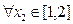 ,总有
,总有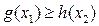 成立,求实数
成立,求实数 的取值范围
的取值范围解:(Ⅰ)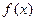 的定义域为
的定义域为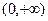 ,且
,且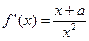 , ----------------1分
, ----------------1分
①当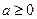 时,
时,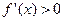 ,
,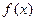 在
在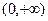 上单调递增; ----------------2分
上单调递增; ----------------2分
②当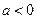 时,由
时,由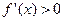 ,得
,得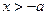 ;由
;由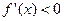 ,得
,得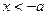 ;
;
故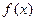 在
在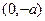 上单调递减,在
上单调递减,在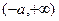 上单调递增. ----------------4分
上单调递增. ----------------4分
(Ⅱ)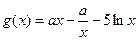 ,
,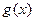 的定义域为
的定义域为
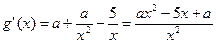 ----------------5分
----------------5分
因为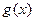 在其定义域内为增函数,所以
在其定义域内为增函数,所以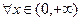 ,
,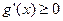
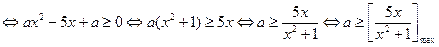
而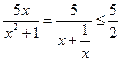 ,当且仅当
,当且仅当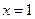 时取等号,
时取等号,
所以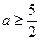 ----------------8分
----------------8分
(Ⅲ)当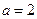 时,
时,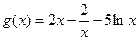 ,
,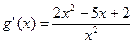
由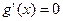 得
得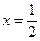 或
或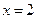
当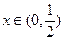 时,
时,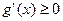 ;当
;当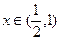 时,
时,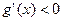 .
.
所以在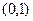 上,
上, ----------------10分
----------------10分
而“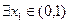 ,
,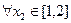 ,总有
,总有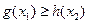 成立”等价于
成立”等价于
“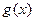 在
在 上的最大值不小于
上的最大值不小于 在
在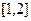 上的最大值”
上的最大值”
而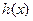 在
在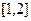 上的最大值为
上的最大值为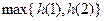
所以有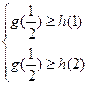 -----------------------------------------------------------------------------12分
-----------------------------------------------------------------------------12分
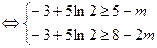
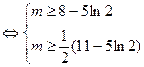
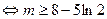
所以实数 的取值范围是
的取值范围是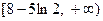 ------------------------------------------------------------13分
------------------------------------------------------------13分
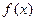 的定义域为
的定义域为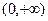 ,且
,且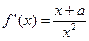 , ----------------1分
, ----------------1分①当
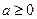 时,
时,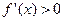 ,
,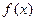 在
在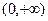 上单调递增; ----------------2分
上单调递增; ----------------2分②当
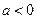 时,由
时,由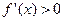 ,得
,得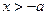 ;由
;由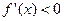 ,得
,得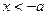 ;
;故
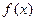 在
在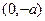 上单调递减,在
上单调递减,在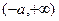 上单调递增. ----------------4分
上单调递增. ----------------4分(Ⅱ)
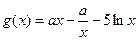 ,
,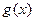 的定义域为
的定义域为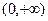
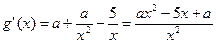 ----------------5分
----------------5分因为
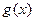 在其定义域内为增函数,所以
在其定义域内为增函数,所以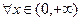 ,
,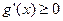
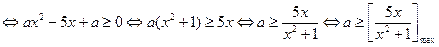
而
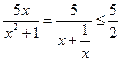 ,当且仅当
,当且仅当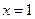 时取等号,
时取等号,所以
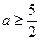 ----------------8分
----------------8分(Ⅲ)当
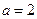 时,
时,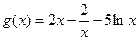 ,
,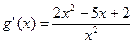
由
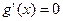 得
得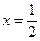 或
或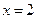
当
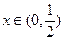 时,
时,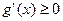 ;当
;当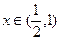 时,
时,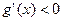 .
.所以在
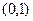 上,
上, ----------------10分
----------------10分而“
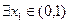 ,
,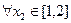 ,总有
,总有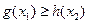 成立”等价于
成立”等价于“
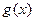 在
在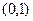 上的最大值不小于
上的最大值不小于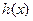 在
在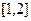 上的最大值”
上的最大值”而
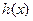 在
在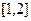 上的最大值为
上的最大值为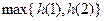
所以有
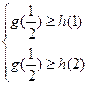 -----------------------------------------------------------------------------12分
-----------------------------------------------------------------------------12分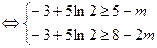
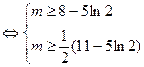
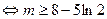
所以实数
 的取值范围是
的取值范围是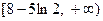 ------------------------------------------------------------13分
------------------------------------------------------------13分略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
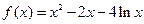 ,则
,则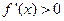 的解集为( )
的解集为( )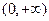
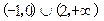
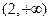
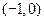
 是
是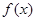 的导函数,
的导函数,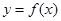 的图象
的图象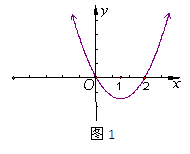
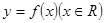 是可导的函数,若满足
是可导的函数,若满足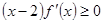 ,则必有
,则必有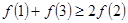
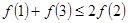
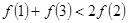
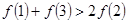
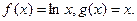
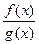 的单调性并求其最大值
的单调性并求其最大值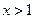 ,求证:
,求证: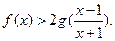
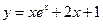 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为 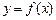 的定义域为
的定义域为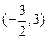 ,且
,且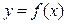 的图像如右图所示,记
的图像如右图所示,记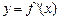 ,则不等式
,则不等式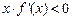 的解集是 ▲ .
的解集是 ▲ .