题目内容
已知函数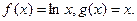
(1)讨论函数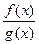 的单调性并求其最大值
的单调性并求其最大值
(2)若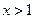 ,求证:
,求证: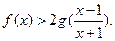
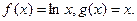
(1)讨论函数
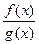 的单调性并求其最大值
的单调性并求其最大值(2)若
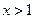 ,求证:
,求证: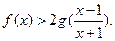
解:(1) ……………………………………2分
……………………………………2分
因为当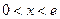 时,
时, ,所以
,所以 是函数的递增区间;…………4分
是函数的递增区间;…………4分
当 时,
时,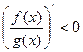 ,所以
,所以 是函数的递减区间;…………5分
是函数的递减区间;…………5分
显然,当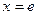 时,函数
时,函数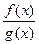 有最大值,最大值为
有最大值,最大值为 ………………6分。
………………6分。
(2)令 则
则 ,
,
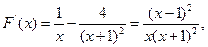 ………………………………………………9分
………………………………………………9分
当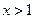 时,
时, ,所以
,所以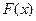 在(1,+∞)上为增函数。
在(1,+∞)上为增函数。
所以当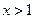 时,
时,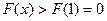 ,
,
故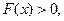 即
即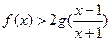 ………………………………………………12分
………………………………………………12分
 ……………………………………2分
……………………………………2分因为当
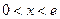 时,
时, ,所以
,所以 是函数的递增区间;…………4分
是函数的递增区间;…………4分当
 时,
时,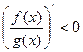 ,所以
,所以 是函数的递减区间;…………5分
是函数的递减区间;…………5分显然,当
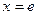 时,函数
时,函数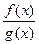 有最大值,最大值为
有最大值,最大值为 ………………6分。
………………6分。(2)令
 则
则 ,
,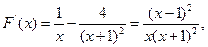 ………………………………………………9分
………………………………………………9分当
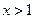 时,
时, ,所以
,所以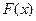 在(1,+∞)上为增函数。
在(1,+∞)上为增函数。所以当
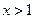 时,
时,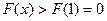 ,
,故
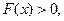 即
即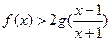 ………………………………………………12分
………………………………………………12分略

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
 ,
,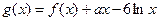 ,其中
,其中 R
R 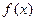 的单调性
的单调性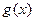 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围
的取值范围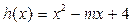 , 当
, 当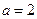 时,若
时,若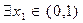 ,
,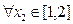 ,总有
,总有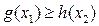 成立,求实数
成立,求实数 的取值范围
的取值范围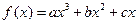 的极小值为
的极小值为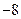 ,其导函数
,其导函数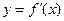 的图像开口向下且经过点
的图像开口向下且经过点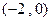 ,
,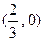
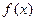 的解析式;(Ⅱ)方程
的解析式;(Ⅱ)方程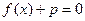 有唯一实数解,求
有唯一实数解,求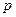 的取值范围
的取值范围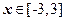 都有
都有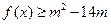 恒成立,求实数
恒成立,求实数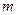 的取值范围
的取值范围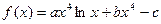 (
(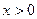 )在
)在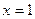 处取得极值
处取得极值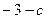 ,其中
,其中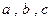 为常数
为常数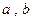 的值; (2)讨论函数
的值; (2)讨论函数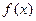 的单调区间
的单调区间 恒成立,求
恒成立,求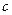 的取值范围
的取值范围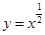 ,②
,②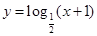 ,③
,③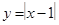 ,④
,④ ,其中在
,其中在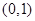 上单调递减的函数序号是( )
上单调递减的函数序号是( )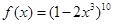 ,则
,则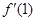 等于
等于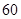
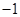
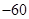
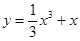 在点
在点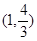 处的切线与坐标轴围成的三角形的面积为( )
处的切线与坐标轴围成的三角形的面积为( )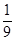
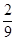
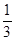
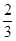
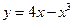 在点
在点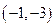 处的切线方程是
处的切线方程是 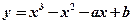 在
在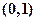 处的切线方程为
处的切线方程为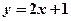 ,则
,则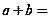 _
_