题目内容
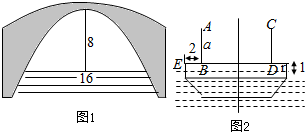
6.如图1,一座抛物线型拱桥,水面离拱顶8m,水面宽16m,如图2,一艘船的宽度为12m,船的甲板与水面距离为1m,船上两根高为a m的杆垂直于船的甲板,且到甲板左右两边的距离为2m,现船正面正对桥洞(船截面的中轴线与抛物线对称轴重合时)通过该拱桥(1)当a=3时,该渔船是否能安全通过该拱桥?
(2)若该渔船能安全通过该拱桥,求a的最大值.
分析 (1)通过设抛物线型拱桥方程为y=f(x)=mx2+n,代入易知点的坐标计算可知抛物线型拱桥方程,进而比较f(-4)与4的大小关系即可;
(2)通过(1)可知,要使该渔船能安全通过该拱桥只需f(-4)≤a+1,进而计算可得结论.
解答 解:(1)设抛物线型拱桥方程为:y=f(x)=mx2+n,
依题意,$\left\{\begin{array}{l}{m•{8}^{2}+n=0}\\{0+n=8}\end{array}\right.$,
解得:m=-$\frac{1}{8}$,n=8,
∴抛物线型拱桥方程为:y=f(x)=-$\frac{1}{8}$x2+8,
建系如图,则E(-6,1),A(-4,4),
∵f(-6)=$\frac{7}{2}$,f(-4)=6,
∴当a=3时,该渔船能安全通过该拱桥;
(2)由(1)可知,要使该渔船能安全通过该拱桥,
则f(-4)≤a+1,
即a≥6-1=5,
∴a的最大值为5米.
点评 本题考查直线与圆锥曲线的关系,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
11.若0<a<1,-1<b<0,则函数y=ax+b的图象必不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |