题目内容
5．求证：等腰梯形的对角线相等．分析 等腰梯形ABCD中，AD∥BC，AB=DC，欲证AC=BD，只需证明△ABC≌△DCB即可．
解答 已知：等腰梯形ABCD中，AD∥BC，AB=DC，
求证：AC=BD．
证明：等腰梯形ABCD中，
∵AD∥BC，AB=DC，
∴∠ABC=∠DCB，
又∵BC=CB，∴△ABC≌△DCB，
∴AC=DB．
点评 本题考查等腰梯形的对角线相等的证明，是基础题，解题时要认真审题，注意三角形全等的判定定理及等腰梯形的性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
15．函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1（x≥0）}\\{f（x+1）（x＜0）}\end{array}\right.$，若方程f（x）=-x+a有且只有两个不等的实数根，则实数a的取值范围为（ ）
| A． | （-∞，0） | B． | [0，1） | C． | （-∞，1） | D． | [0，+∞） |
13．若点A（-2，m）在正比例函数y=-$\frac{1}{2}$x的图象上，则m的值是（ ）
| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | 1 | D． | -1 |
20．直线l：4x-y-4=0与l1：x-2y-2=0及l2：4x+3y-12=0所得两交点的距离为（ ）
| A． | $\frac{3\sqrt{17}}{2}$ | B． | $\frac{6}{7}$$\sqrt{17}$ | C． | 3$\sqrt{17}$ | D． | $\frac{9}{14}$$\sqrt{17}$ |
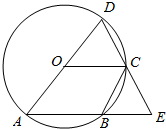如图，AD是⊙O的直径，B为⊙O上的一点，连接AB并延长至点E，使得AE=AD，连接DE，交⊙O于点C，连接OC．