题目内容
5.已知α,b,c均为正数,且a+b+2c=1,则$\frac{1}{a+b}+\frac{1}{c}$的最小值是3+2$\sqrt{2}$.分析 由题意可得$\frac{1}{a+b}+\frac{1}{c}$=($\frac{1}{a+b}+\frac{1}{c}$)[(a+b)+2c]=3+$\frac{2c}{a+b}$+$\frac{a+b}{c}$,由基本不等式可得.
解答 解:∵α,b,c均为正数,且(a+b)+2c=1,
∴$\frac{1}{a+b}+\frac{1}{c}$=($\frac{1}{a+b}+\frac{1}{c}$)[(a+b)+2c]
=3+$\frac{2c}{a+b}$+$\frac{a+b}{c}$≥3+2$\sqrt{\frac{2c}{a+b}•\frac{a+b}{c}}$=3+2$\sqrt{2}$
当且仅当$\frac{2c}{a+b}$=$\frac{a+b}{c}$即a+b=$\sqrt{2}$c时取等号.
故答案为:3+2$\sqrt{2}$.
点评 本题考查基本不等式求最值,整体代入是解决问题的关键,属基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.已知lg2=a,1g7=b,则log1498=( )
| A. | $\frac{a-b}{a+b}$ | B. | $\frac{2a+b}{a+b}$ | C. | $\frac{a-2b}{a+b}$ | D. | $\frac{a+2b}{a+b}$ |
13.在复平面内,复数z=$\frac{1}{1-i}$+i2对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
17.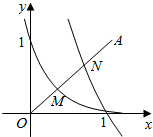 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
 如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )
如图,点O为坐标原点,点A(1,1),若函数y=ax(a>0,且a≠1)及logbx(b>0,且b≠1)的图象与线段OA分别交于点M,N,且M,N恰好是线段OA的两个三等分点,则a,b满足( )| A. | a<b<1 | B. | b<a<1 | C. | b>a>1 | D. | a>b>1 |