题目内容
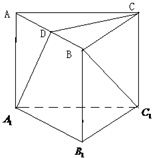 已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1
已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1(1)求证:BC1∥平面CA1D
(2)求证:平面CA1D⊥平面AA1B1B
(3)求二面角C-DA1-C1的余弦值.
分析:(1)设AC1与A1C交于O,连接DO,则可得O为AC1的中点,则由OD∥BC1结合线面平行的判定定理可证
(2)根据面面垂直的判定定理可证,要证明平面CA1D⊥平面AA1B1B,结合已知,只要先证BB1⊥CD,CD⊥AB,进而有CD⊥平面AA1B1B,根据面面垂直的判定定理即可证
(3)设AC=BC=BB1=a,,通过计算可得A1D⊥DC
过C1作C1M⊥A1D垂足为M,则可得
=
,过M作MN∥DC与A1C交于N,则MN⊥A1D,则∠NMC1即为二面角角C-DA1-C1的平面角,在△MNC1中,由余弦定理可得,cos∠C1MN=
可求
(2)根据面面垂直的判定定理可证,要证明平面CA1D⊥平面AA1B1B,结合已知,只要先证BB1⊥CD,CD⊥AB,进而有CD⊥平面AA1B1B,根据面面垂直的判定定理即可证
(3)设AC=BC=BB1=a,,通过计算可得A1D⊥DC
过C1作C1M⊥A1D垂足为M,则可得
| A1M |
| MD |
| 1 |
| 2 |
| MN2+MC12-C1N2 |
| 2MN•MC1 |
解答:证明:(1)设AC1与A1C交于O,连接DO,则可得O为AC1的中点
所以OD∥BC1
因为DO?平面CA1D,BC1?平面CA1D
所以BC1∥平面CA1D
(2)由直三棱柱ABC-可得BB1⊥平面ABC
所以BB1⊥CD
又AC=BC,D为AB的中点∴CD⊥AB
∵AB∩BB1=B
∴CD⊥平面AA1B1B
又∵CD?平面CA1D
∴平面CA1D⊥平面AA1B1B
(3)解:设AC=BC=BB1=a,则可得A1D=
a,DC=
a,A1C=
a
∴A1D2+DC2=A1C2,即A1D⊥DC
在△C1DA1中,AD=C1D=
a,A1C1=a
过C1作C1M⊥A1D垂足为M,则可得
=
,过M作MN∥DC与A1C交于N,则MN⊥A1D
∴∠NMC1即为二面角角C-DA1-C1的平面角
在△MNC1中,MC1=
a,C1N=
a,MN=
a
由余弦定理可得,cos∠C1MN=
=
所以OD∥BC1
因为DO?平面CA1D,BC1?平面CA1D
所以BC1∥平面CA1D
(2)由直三棱柱ABC-可得BB1⊥平面ABC
所以BB1⊥CD
又AC=BC,D为AB的中点∴CD⊥AB
∵AB∩BB1=B
∴CD⊥平面AA1B1B
又∵CD?平面CA1D
∴平面CA1D⊥平面AA1B1B
(3)解:设AC=BC=BB1=a,则可得A1D=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴A1D2+DC2=A1C2,即A1D⊥DC
在△C1DA1中,AD=C1D=
| ||
| 2 |
过C1作C1M⊥A1D垂足为M,则可得
| A1M |
| MD |
| 1 |
| 2 |
∴∠NMC1即为二面角角C-DA1-C1的平面角
在△MNC1中,MC1=
| ||
| 6 |
| ||
| 3 |
| ||
| 6 |
由余弦定理可得,cos∠C1MN=
| MN2+MC12-C1N2 |
| 2MN•MC1 |
-3
| ||
| 5 |
点评:本题是一道综合性较强的试题,综合考查了线面平行(垂直)的判定定理的应用及线线平行(垂直),线面平行(垂直),面面平行(垂直)的相互转化,难点在于二面角的求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.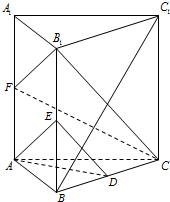 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.