题目内容
(本题满分14分)如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点E为
,点E为 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: ;
;
(III)在线段AB上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出
的长;若不存在,请说明理由.
【答案】
(1)见解析;(2)见解析;(3) .
.
【解析】第一问中利用线面平行的判定定理可知,只要证明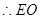 //
// ,那么可以得证。
,那么可以得证。
第二问中,利用线面垂直度性质定理得到线线垂直关系是证明

第三问中,假设存在点点 ,使二面角
,使二面角 的大小为
的大小为 ,可以建立空间直角坐标系,借助于法向量的夹角表示二面角的平面角的大小得到点的坐标。
,可以建立空间直角坐标系,借助于法向量的夹角表示二面角的平面角的大小得到点的坐标。
解:(Ⅰ) , 点E为
, 点E为 的中点,连接
的中点,连接 。
。

 的中位线
的中位线 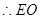 //
// ……2分
……2分
又

 …………4分
…………4分
(II)正方形 中,
中, ,
由已知可得:
,
由已知可得: ,
,

 ,
,

 ………………………9分
………………………9分
(Ⅲ)由题意可得: ,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则
,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则 ,
,

设 ,
,
设平面 的法向量为
的法向量为 ,
,
则 得
得 ,
,
取平面 的一个法向量
的一个法向量 ,
,
而平面 的一个法向量为
的一个法向量为 ,二面角
,二面角 的大小为
的大小为 ,
, ,
,
故当 时,二面角
时,二面角 的大小为
的大小为 ………………………14分
………………………14分

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;